题目内容
设不等式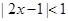 的解集为
的解集为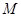 .(I)求集合
.(I)求集合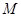 ;(II)若
;(II)若 ,
, ∈
∈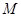 ,试比较
,试比较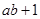 与
与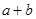 的大小.
的大小.
(I) (II)
(II)
解析试题分析:(I)由 所以
所以
(II)由(I)和 ,所以
,所以 故
故
考点:绝对值不等式的解法,不等式的性质。
点评:简单题,绝对值不等式的解法,往往从“去”绝对值的符号入手,主要方法有“平方法”“分类讨论法”,有时利用绝对值的几何意义,会简化解题过程。比较大小问题,常常利用“差比法”—作差---变形---定号。

练习册系列答案
相关题目
题目内容
设不等式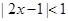 的解集为
的解集为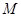 .(I)求集合
.(I)求集合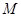 ;(II)若
;(II)若 ,
, ∈
∈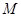 ,试比较
,试比较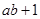 与
与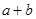 的大小.
的大小.
(I) (II)
(II)
解析试题分析:(I)由 所以
所以
(II)由(I)和 ,所以
,所以 故
故
考点:绝对值不等式的解法,不等式的性质。
点评:简单题,绝对值不等式的解法,往往从“去”绝对值的符号入手,主要方法有“平方法”“分类讨论法”,有时利用绝对值的几何意义,会简化解题过程。比较大小问题,常常利用“差比法”—作差---变形---定号。
