题目内容
解不等式(组)
(1)
(2)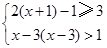
(1)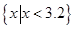 (2)
(2)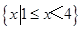
解析试题分析:(1)由原不等式可得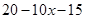 <
<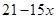 ……2分
……2分
化简得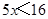 , ……3分
, ……3分
即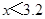 ,所以原不等式的解集为
,所以原不等式的解集为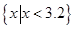 . ……4分 (2)解不等式①得:
. ……4分 (2)解不等式①得: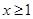 ……5分
……5分
解不等式②得: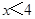 ……6分
……6分
∴原不等式组的解集为: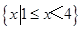 . ……8分
. ……8分
考点:本小题主要考查分式不等式和不等式组的求解.
点评:解集此类问题的关键是灵活变形,变形时注意变形的等价性,解方程组求交集时可以借助数轴辅助解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列结论正确的是( ).
A.当x>0且x≠1时,lgx+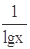 ≥2 ≥2 |
B.当x>0时,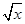 + +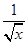 ≥2 ≥2 |
C.x≥2时,x+ 的最小值为2 的最小值为2 |
D.当0<x≤2时,x- 无最大值 无最大值 |
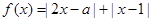 .
.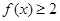 的解集;
的解集;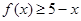 对
对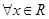 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.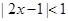 的解集为
的解集为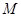 .(I)求集合
.(I)求集合 ,
, ∈
∈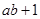 与
与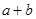 的大小.
的大小.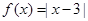 ,
,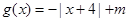
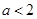 ,解关于
,解关于 的不等式
的不等式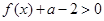 ;
; 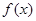 的图象恒在函数
的图象恒在函数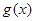 图象的上方,求实数
图象的上方,求实数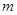 的取值范围.
的取值范围.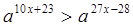
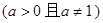 中的x的取值范围.
中的x的取值范围.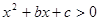 的解集为
的解集为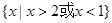
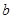 和
和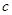 的值; (2)求不等式
的值; (2)求不等式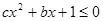 的解集.
的解集.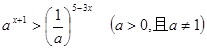 ,求
,求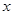 的取值范围.
的取值范围.