题目内容
17．若$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$都是单位向量，且$\overrightarrow{p}$=$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$，试求|$\overrightarrow{p}$|的取值范围．分析 0≤|$\overrightarrow{a}+\overrightarrow{b}$|≤2，故当$\overrightarrow{a}+\overrightarrow{b}$=-$\overrightarrow{c}$时，|$\overrightarrow{p}$|取得最小值0，当$\overrightarrow{a}+\overrightarrow{b}$=2$\overrightarrow{c}$时，|$\overrightarrow{p}$|取得最大值．
解答 解：∵0≤|$\overrightarrow{a}+\overrightarrow{b}$|≤2，∴当$\overrightarrow{a}+\overrightarrow{b}$=-$\overrightarrow{c}$时，|$\overrightarrow{p}$|=0；
当$\overrightarrow{a}+\overrightarrow{b}$=2$\overrightarrow{c}$时，|$\overrightarrow{p}$|=|3$\overrightarrow{c}$|=3．
∴0≤|$\overrightarrow{p}$|≤3．
点评 本题考查了平面向量的模长计算，属于基础题．
练习册系列答案
相关题目
7．已知函数f（x）=|sinx|+|cosx|，则下列结论中错误的是（ ）
| A． | f（x）是周期函数 | B． | f（x）的对称轴方程为x=$\frac{kπ}{4}$，k∈Z | ||
| C． | f（x）在区间（$\frac{π}{4}$，$\frac{3π}{4}$）上为增函数 | D． | 方程f（x）=$\frac{6}{5}$在区间[-$\frac{3}{2}$π，0]上有6个根 |
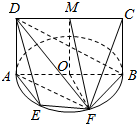如图所示，矩形ABCD所在的平面垂直圆O所在的平面，AB是圆O的直径，M是CD上一点，且DM=EF，E、F是圆O上的点，∠EAF=∠FAB=30°．