题目内容
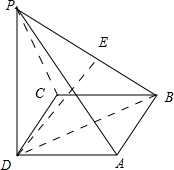
在四棱锥P-ABCD中,底面ABCD是平行四边形,BD=4,PD⊥平面ABCD,平面PBC⊥平面PBD,二面角P-BC-D为60°.
(1)求证:BC⊥BD;
(2)求点A到平面PBC的距离.
(1)求证:BC⊥BD;
(2)求点A到平面PBC的距离.
考点:直线与平面垂直的性质,向量语言表述线线的垂直、平行关系
专题:空间位置关系与距离
分析:(1)过D向PB作垂线,垂足为E,先证明出DE⊥平面PBC,利用线面垂直的性质证明出DE⊥BC,根据PD⊥平面ABCD,推断出PD⊥BC,继而可利用线面垂直的判定定理证明出BC⊥平面PBD,进而可知BC⊥BD;
(2)先证明出AD∥平面PBC,推断点A到平面PBC的距离与点D到平面PBC的距离相等,继而证明出DB的长度即为点D到平面PBC的距离,证明出∠PBD为二面角P-BC-D的平面角,则DE可求.
(2)先证明出AD∥平面PBC,推断点A到平面PBC的距离与点D到平面PBC的距离相等,继而证明出DB的长度即为点D到平面PBC的距离,证明出∠PBD为二面角P-BC-D的平面角,则DE可求.
解答:
(1)证明:过D向PB作垂线,垂足为E,
∵平面PBC⊥平面PBD,平面PBC∩平面PBD=PB,
∴DE⊥平面PBC,
∵BC?平面PBC,
∴DE⊥BC,
∵PD⊥平面ABCD,BC?平面ABCD,
∴PD⊥BC,
∵PD?平面PBD,DE?平面PBD,DE∩PD=D,
∴BC⊥平面PBD,
∵BD?平面PBD,
∴BC⊥BD,
(2)∵AD∥BC,BC?平面PBC,AD?平面PBC,
∴AD∥平面PBC,
∴点A到平面PBC的距离与点D到平面PBC的距离相等,
∵DE⊥平面PBC,
∴DB的长度即为点D到平面PBC的距离,
∵BC⊥平面PBD,
∴BC⊥BD,BC⊥PB,
∴∠PBD为二面角P-BC-D的平面角,即∠PBD=60°,
∴在Rt△DBE中,DE=
BD=2
,
即点A到平面PBC的距离为2
.
∵平面PBC⊥平面PBD,平面PBC∩平面PBD=PB,
∴DE⊥平面PBC,
∵BC?平面PBC,
∴DE⊥BC,
∵PD⊥平面ABCD,BC?平面ABCD,
∴PD⊥BC,
∵PD?平面PBD,DE?平面PBD,DE∩PD=D,
∴BC⊥平面PBD,
∵BD?平面PBD,
∴BC⊥BD,
(2)∵AD∥BC,BC?平面PBC,AD?平面PBC,
∴AD∥平面PBC,
∴点A到平面PBC的距离与点D到平面PBC的距离相等,
∵DE⊥平面PBC,
∴DB的长度即为点D到平面PBC的距离,
∵BC⊥平面PBD,
∴BC⊥BD,BC⊥PB,
∴∠PBD为二面角P-BC-D的平面角,即∠PBD=60°,
∴在Rt△DBE中,DE=
| ||
| 2 |
| 3 |
即点A到平面PBC的距离为2
| 3 |

点评:本题主要考查了线面垂直的判定定理和性质的应用.作出DE的辅助线解决本题的关键所在.

练习册系列答案
相关题目
 人民日报3月14日报道,中国人民银行已下发通知,要求暂停二维码(条码)支付,虚拟信用卡等支付业务和产品.前不久,某调研机构调研了在校大学生网上购物的情况,随机调查了16位在校大学生的网购比例,结果如茎叶图所示(图中茎7叶3表示73%,其余相同):
人民日报3月14日报道,中国人民银行已下发通知,要求暂停二维码(条码)支付,虚拟信用卡等支付业务和产品.前不久,某调研机构调研了在校大学生网上购物的情况,随机调查了16位在校大学生的网购比例,结果如茎叶图所示(图中茎7叶3表示73%,其余相同):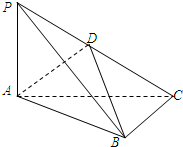 在三棱锥P-ABC中,PA⊥平面ABC,AP=AB=
在三棱锥P-ABC中,PA⊥平面ABC,AP=AB=