题目内容
12.若1oga$\frac{2}{3}$<0,则实数a的取值范围是( )| A. | ($\frac{2}{3}$,1) | B. | ($\frac{2}{3}$,+∞) | C. | (0,1) | D. | (1,+∞) |
分析 根据对数函数的定义与性质,即可得出1oga$\frac{2}{3}$<0时a的取值范围.
解答 解:根据对数函数的定义与性质,得;
当a>1时,1oga$\frac{2}{3}$<0恒成立,
当1>a>0时,1oga$\frac{2}{3}$>0恒成立,
所以1oga$\frac{2}{3}$<0时a的取值范围是(1,+∞).
故选:D.
点评 本题考查了利用对数函数的定义与性质求不等式解集的应用问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知f(x-1)=2x,则f(3)=( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
7.设实数x,y满足$\left\{\begin{array}{l}{2x-y+1≤0}\\{y≤-x-k}\\{x≥0}\end{array}\right.$(k为常数),若目标函数z=3x-y的最大值为-$\frac{1}{3}$,则点(x,y)构成的平面区域Ω的面积为( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 2 | D. | 4 |
1.投掷一枚均匀骰子,记“骰子向上的点数是偶数”为事件A,“骰子向上的点数6”为事件B,则事件A,B中至少有一件发生的概率是( )
| A. | $\frac{5}{12}$ | B. | $\frac{1}{2}$ | C. | $\frac{7}{12}$ | D. | $\frac{2}{3}$ |
16.执行如图所示的程序框图后,输出的结果为( )
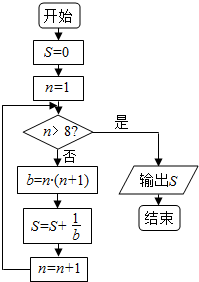

| A. | $\frac{7}{8}$ | B. | $\frac{9}{10}$ | C. | $\frac{8}{9}$ | D. | $\frac{10}{11}$ |