0.1.1.2.2.2.2七个数字全取排成七位数.有90种方法．题目和参考答案——青夏教育精英家教网—

题目内容

17．0、1、1、2、2、2、2七个数字全取排成七位数，有90种方法．

分析不考虑首位是0，有$\frac{{A}_{7}^{7}}{{A}_{2}^{2}{A}_{4}^{4}}$=105种方法；首位是0，有$\frac{{A}_{6}^{6}}{{A}_{2}^{2}{A}_{4}^{4}}$=15种方法，即可得出结论．

解答解：不考虑首位是0，有$\frac{{A}_{7}^{7}}{{A}_{2}^{2}{A}_{4}^{4}}$=105种方法；首位是0，有$\frac{{A}_{6}^{6}}{{A}_{2}^{2}{A}_{4}^{4}}$=15种方法，
∴共有105-15=90种方法．
故答案为：90．

点评本题考查排列知识的运用，考查学生的计算能力，比较基础．

练习册系列答案

8．在标准化的考试中既有单选题又有多选题，多选题是从A，B，C，D四个选项中选出所有正确的答案（正确答案可能是一个或多个选项），有一道多选题考生不会做，若他随机作答，则他答对的概率是（　　）

5．

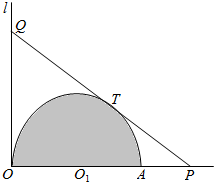如图，阴影部分为古建筑物保护群所在地，其形状是以O₁为圆心，半径为1km的半圆面．公路l经过点O，且与直径OA垂直，现计划修建一条与半圆相切的公路PQ（点P在直径OA的延长线上，点Q在公路l上），T为切点．
（1）按下列要求建立函数关系：
①设∠OPQ=α（rad），将△OPQ的面积S表示为α的函数；
②设OQ=t（km），将△OPQ的面积S表示为t的函数．
（2）请你选用（1）中的一个函数关系，求△OPQ的面积S的最小值．

12．若1og_a$\frac{2}{3}$＜0，则实数a的取值范围是（　　）

2．已知tanα=-$\frac{1}{3}$，且α是第四象限．
（1）若P为α角终边上的一点，写出符合条件的一个P点坐标；
（2）求sinα，cosα的值．

9．已知函数f（x）=（x-t）²+（e^2x-2t）²，x∈R，其中参数t∈R，则函数f（x）的最小值为（　　）

$\frac{2\sqrt{5}}{5}$

6．若10^a=2，10^b=3，则10^a-2b=$\frac{2}{9}$．

1．已知函数f（x）=x³+ax²+bx（a，b∈R）的图象与直线y=0在原点处相切，函数f（x）有极小值-$\frac{4}{27}$，则a的值为-1．

试题分类