题目内容
光线从A(-3,5)射到直线l:x-y+4=0上发生反射,反射光线过点B(0,6),求入射光线和反射光线的方程.
考点:与直线关于点、直线对称的直线方程
专题:直线与圆
分析:由对称性可得A(-3,5)关于直线l的对称点为A′的坐标,进而可得反射光线的方程,可解入射点,可得射光线的方程.
解答:
解:设A(-3,5)关于直线l的对称点为A′(a,b),
则可得
,解得
,即A′(1,1),
由反射原理可知反射光线为A′B,斜率k=
=-5,
∴反射光线的方程为y-6=-5(x-0),即5x+y-6=0,
联立方程
,解得
,即入射点C(
,
),
∴入射光线AC的斜率k′=
=-
,
∴入射光线的方程为y-5=-
(x+3),即x+5y-22=0
则可得
|
|
由反射原理可知反射光线为A′B,斜率k=
| 6-1 |
| 0-1 |
∴反射光线的方程为y-6=-5(x-0),即5x+y-6=0,
联立方程
|
|
| 1 |
| 3 |
| 13 |
| 3 |
∴入射光线AC的斜率k′=
| ||
|
| 1 |
| 5 |
∴入射光线的方程为y-5=-
| 1 |
| 5 |
点评:本题考查直线的对称性,涉及垂直平分线的性质,属基础题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
已知x,y∈R,若p:x<1且y<1,q:x+y≥2.则p是¬q的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |

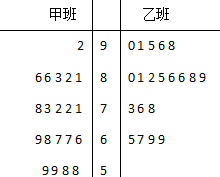 我市某校某数学老师这学期分别用m,n两种不同的教学方式试验高一甲、乙两个班(人数均为60人,入学数学平均分和优秀率都相同,勤奋程度和自觉性都一样).现随机抽取甲、乙两班各20名的数学期末考试成绩,并作出茎叶图如图所示.
我市某校某数学老师这学期分别用m,n两种不同的教学方式试验高一甲、乙两个班(人数均为60人,入学数学平均分和优秀率都相同,勤奋程度和自觉性都一样).现随机抽取甲、乙两班各20名的数学期末考试成绩,并作出茎叶图如图所示.