题目内容
已知正项数列{xn}满足xn+
<2(n∈N*).
(1)证明:xn+
≥2;
(2)证明:xn<xn+1;
(3)用数学归纳法证明:xn>
.
| 1 |
| xn+1 |
(1)证明:xn+
| 1 |
| xn |
(2)证明:xn<xn+1;
(3)用数学归纳法证明:xn>
| n-1 |
| n |
考点:数学归纳法
专题:推理和证明
分析:(1)可以利用基本不等式进行证明;(2)利用(1)的结论,通过不等式传递,得到本题结果;(3)可以将原不等式利用数学归纳法进行证明.
解答:
证明:(1)∵xn>0,∴xn+
≥2
=2,∴xn+
≥2;,当且仅当xn=1时,等号成立.
(2)由(1)知xn+
≥2,又xn+
<2,
所以
>
,所以xn<xn+1.
(3)①当n=1时,不等式显然成立;
②假设当n=k(k∈N*)时不等式成立,即xk>
.
当n=k+1时,由xn+
<2,得xk+1>
>
=
,
即当n=k+1时,不等式成立;
综上,对一切n∈N*都有xn>
成立.
| 1 |
| xn |
xn×
|
| 1 |
| xn |
(2)由(1)知xn+
| 1 |
| xn |
| 1 |
| xn+1 |
所以
| 1 |
| xn |
| 1 |
| xn+1 |
(3)①当n=1时,不等式显然成立;
②假设当n=k(k∈N*)时不等式成立,即xk>
| k-1 |
| k |
当n=k+1时,由xn+
| 1 |
| xn+1 |
| 1 |
| 2-xk |
| 1 | ||
2-
|
| k |
| k+1 |
即当n=k+1时,不等式成立;
综上,对一切n∈N*都有xn>
| n-1 |
| n |
点评:本题考查的不等式和数列的知识,包括基本不等式、解不等式、数列、数学归纳法,思维量较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 某公司为一家制冷设备厂设计生产一种长方形薄板,其周长为4米,这种薄板须沿其对角线折叠后使用.如图所示,ABCD(AB>AD)为长方形薄板,沿AC折叠后,AB折痕为AB′,AB′交DC于点P,当凹多边形ACB′PD的面积最大时制冷效果最好.
某公司为一家制冷设备厂设计生产一种长方形薄板,其周长为4米,这种薄板须沿其对角线折叠后使用.如图所示,ABCD(AB>AD)为长方形薄板,沿AC折叠后,AB折痕为AB′,AB′交DC于点P,当凹多边形ACB′PD的面积最大时制冷效果最好.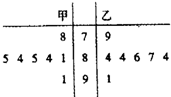 为迎接2013年全运会在注著名的海滨城市大连举行了场奥运选拔赛,其中甲乙两名运动员为争取最好一个参赛名额进行了7轮比赛的得分如茎叶图所示.
为迎接2013年全运会在注著名的海滨城市大连举行了场奥运选拔赛,其中甲乙两名运动员为争取最好一个参赛名额进行了7轮比赛的得分如茎叶图所示.