题目内容
已知椭圆C:
+
=1(a>b>0)过点(1,
),且离心率e=
.
(1)求椭圆方程;
(2)若直线l:y=
x+m与椭圆交于不同的两点M,N,且线段MN的垂直平分线过定点G(
,0),求直线l的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 1 |
| 2 |
(1)求椭圆方程;
(2)若直线l:y=
| 1 |
| 2 |
| 1 |
| 8 |
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(1)由题意可得
,解得即可;
(2)设M(x1,y1),N(x2,y2),线段MN的中点为P(x0,y0).联立
,化为x2+mx+m2-3=0,利用根与系数的关系与中点坐标公式可得
P(-
,
).可得线段MN的垂直平分线方程为y-
=-2(x+
),把G(
,0)代入解出m即可.
|
(2)设M(x1,y1),N(x2,y2),线段MN的中点为P(x0,y0).联立
|
P(-
| m |
| 4 |
| 7m |
| 8 |
| 7m |
| 8 |
| m |
| 4 |
| 1 |
| 8 |
解答:
解:(1)∵椭圆C:
+
=1(a>b>0)过点(1,
),且离心率e=
.
∴
,解得a=2,c=1,b2=3.
∴椭圆C的方程为
+
=1.
(2)设M(x1,y1),N(x2,y2),线段MN的中点为P(x0,y0).
联立
,化为x2+mx+m2-3=0,
∴x1+x2=-
,x1x2=m2-3.
∴x0=
=-
,y0=
x0+m=-
+m=
.
∴P(-
,
).
∴线段MN的垂直平分线方程为y-
=-2(x+
),
把G(
,0),代入可得0-
=-2(
+
),
解得m=
.
∴直线l的方程为y-
=-2(x+
),化为8x+4y-1=0.
∴直线l的方程为:8x+4y-1=0.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 1 |
| 2 |
∴
|
∴椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)设M(x1,y1),N(x2,y2),线段MN的中点为P(x0,y0).
联立
|
∴x1+x2=-
| m |
| 2 |
∴x0=
| x1+x2 |
| 2 |
| m |
| 4 |
| 1 |
| 2 |
| m |
| 8 |
| 7m |
| 8 |
∴P(-
| m |
| 4 |
| 7m |
| 8 |
∴线段MN的垂直平分线方程为y-
| 7m |
| 8 |
| m |
| 4 |
把G(
| 1 |
| 8 |
| 7m |
| 8 |
| 1 |
| 8 |
| m |
| 4 |
解得m=
| 2 |
| 3 |
∴直线l的方程为y-
| 7 |
| 12 |
| 1 |
| 6 |
∴直线l的方程为:8x+4y-1=0.
点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、中点坐标关系、线段的垂直平分线的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
如图,在空间四边形ABCD中,AB=BC,CD=DA,E、F、G分别是CD、DA、AC的中点,则( )
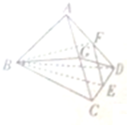

| A、平面BEF⊥平面BGD |
| B、平面ABC⊥平面ACD |
| C、CD⊥平面BEF |
| D、AB⊥平面BGD |
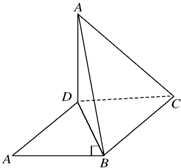 如图,平行四边形ABCD中,AB⊥BD,沿BD将△ABD折起到A′BD,使面A′BD⊥面BCD,连接A′C,则在四面体A′BCD的四个面中,互相垂直的平面有( )
如图,平行四边形ABCD中,AB⊥BD,沿BD将△ABD折起到A′BD,使面A′BD⊥面BCD,连接A′C,则在四面体A′BCD的四个面中,互相垂直的平面有( )