题目内容
14.函数$y={0.3^{|{x^2}-6x+5|}}$的单调增区间为(-∞,1]和[3,5]..分析 首先将解析式中的指数看作一个函数讨论其单调性,然后利用复合函数同增异减的原则讨论原函数的单调性即可.
解答 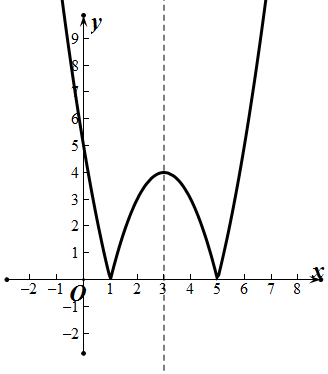 解:绘制函数y=|x2-6x+5|的图象 如图所示:
解:绘制函数y=|x2-6x+5|的图象 如图所示:
观察函数图象可得函数的单调递增区间为:[1,3]和[5,+∞)
单调递减区间为:(-∞,1]和[3,5]
指数函数y=0.3x 在定义域内单调递减,
结合复合函数同增异减的原则可得函数$y={1.3}^{|{x}^{2}-6x+5|}$ 的单调递增区间,
即函数y=|x2-6x+5|的单调递减区间:
(-∞,1]和[3,5].
故答案为:(-∞,1]和[3,5].
点评 本题考查复合函数的单调性,函数图象的变换,指数函数的性质,二次函数的性质等,重点考查学生对基础概念的理解和计算能力,属于基础题.

练习册系列答案
相关题目
19.函数f (x)=2x2-mx+3,当x∈[-2,+∞]时增函数,当x∈(-∞,-2]时是减函数,则f (1)等于( )
| A. | -3 | B. | 13 | ||
| C. | 7 | D. | 由m而定的其它常数 |
6.某几何体的三视图如图所示,则该几何体为( )


| A. | 四棱锥 | B. | 三棱锥 | C. | 三棱柱 | D. | 圆锥 |
3.已知集合A={x||x+1|≤2,B={x|y=lg(x2-x-2)},则A∩∁RB=( )
| A. | [-1,1] | B. | [-3,1] | C. | (-1,1] | D. | [-3,-1] |
 如图所示,在梯形ABCD中,∠A=$\frac{π}{2}$,$AB=\sqrt{2}$,BC=2,$AD=\frac{3}{2}$点E为AB的中点,则$\overrightarrow{CE}•\overrightarrow{BD}$=-2.
如图所示,在梯形ABCD中,∠A=$\frac{π}{2}$,$AB=\sqrt{2}$,BC=2,$AD=\frac{3}{2}$点E为AB的中点,则$\overrightarrow{CE}•\overrightarrow{BD}$=-2. 如图,有一块平行四边形绿地ABCD,经测量BC=2百米,CD=1百米,∠BCD=120°,拟过线段BC上一点E设计一条直路EF(点F在四边形ABCD的边上,不计路的宽度),EF将绿地分成两部分,且右边面积是左边面积的3倍.设EC=x百米,EF=y百米.
如图,有一块平行四边形绿地ABCD,经测量BC=2百米,CD=1百米,∠BCD=120°,拟过线段BC上一点E设计一条直路EF(点F在四边形ABCD的边上,不计路的宽度),EF将绿地分成两部分,且右边面积是左边面积的3倍.设EC=x百米,EF=y百米.