题目内容
14.已知复数z=(2m2-3m-2)+(m2-3m+2)i.(Ⅰ)当实数m取什么值时,复数z是纯虚数;
(Ⅱ)当m=0时,化简$\frac{{z}^{2}}{z+5+2i}$.
分析 (Ⅰ)根据实部等于0,虚部不等于0时,复数z是纯虚数,列出方程组,求解即可得答案;
(Ⅱ)当m=0时,z=-2+2i,把z代入$\frac{{z}^{2}}{z+5+2i}$,由复数代数形式的乘除运算化简即可得答案.
解答 解:(Ⅰ)当$\left\{\begin{array}{l}{2{m}^{2}-3m-2=0}\\{{m}^{2}-3m+2≠0}\end{array}\right.$时,解得$\left\{\begin{array}{l}{m=-\frac{1}{2}或m=2}\\{m≠1且m≠2}\end{array}\right.$,
即$m=-\frac{1}{2}$时,复数z为纯虚数.
(Ⅱ)当m=0时,z=-2+2i,
则$\frac{{z}^{2}}{z+5+2i}$=$\frac{(-2+2i)^{2}}{-2+2i+5+2i}=\frac{-8i}{3+4i}=\frac{-8i(3-4i)}{(3+4i)(3-4i)}$=$\frac{-32-24i}{25}=-\frac{32}{25}-\frac{24}{25}i$.
点评 本题考查了复数代数形式的乘除运算,考查了复数z是纯虚数所具备的条件,是基础题.

练习册系列答案
相关题目
5.直线l把圆x2+y2-2y=0的面积平分,则它被这个圆截得的弦长为( )
| A. | 4 | B. | $\sqrt{2}$ | C. | 2 | D. | 1 |
19.下列从集合A到集合B的对应f是映射的是( )
| A. | A=R,B={x|x是正实数},f:A中的数的绝对值 | |
| B. | A={0,1},B={-1,0,1},f:A中的数的开方 | |
| C. | A=Z,B=Q,f:A中的数的倒数 | |
| D. | A={-1,0,1},B={-1,0,1},f:A中的数的平方 |
6.已知函数f(x)=$\frac{1}{3}$ax3+$\frac{1}{2}$bx2+cx+d,其图象在点(1,f(1))处的切线斜率为0,若a<b<c,且函数f(x)的单调递增区间为(m,n),则n-m的取值范围是( )
| A. | (1,$\frac{3}{2}$) | B. | ($\frac{3}{2}$,3) | C. | (1,3) | D. | (2,3) |
3.命题P:?x∈R,x2>lg1,则P的否定¬P为( )
| A. | ?x0∈R,${{x}_{0}}^{2}$≤lg1 | B. | ?x0∈R,${{x}_{0}}^{2}$<lg1 | ||
| C. | ?x∈R,${{x}_{0}}^{2}$≤lg1 | D. | $?{x_{\;}}∈R,x_{\;}^2<lg1$ |
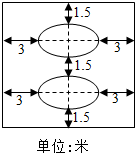 某学校拟在广场上建造一个矩形花园,如图所示,中间是完全相同的两个椭圆型花坛,每个椭圆型花坛的面积均为216π平方米,两个椭圆花坛的距离是1.5米.整个矩形花坛的占地面积为S.
某学校拟在广场上建造一个矩形花园,如图所示,中间是完全相同的两个椭圆型花坛,每个椭圆型花坛的面积均为216π平方米,两个椭圆花坛的距离是1.5米.整个矩形花坛的占地面积为S.