题目内容
已知集合A={0,1,2},B={x|ax+1=0},且A∪B=A,则实数a的取值集合是( )
A、{-1,-
| ||
| B、{-1,-2} | ||
| C、{0,-1,-2} | ||
D、{0,-1,-
|
考点:并集及其运算
专题:集合
分析:利用交集的定义和分类讨论思想求解.
解答:
解:∵集合A={0,1,2},B={x|ax+1=0},且A∪B=A,
∴B=∅,或B={1},或B={2},
当B=∅时,-
不存在,解得a=0;
当B={1}时,-
=1,解得a=-1;
当B={2}时,-
=2,解得a=-
.
∴实数a的取值集合是{0,-1,-
}.
故选:D.
∴B=∅,或B={1},或B={2},
当B=∅时,-
| 1 |
| a |
当B={1}时,-
| 1 |
| a |
当B={2}时,-
| 1 |
| a |
| 1 |
| 2 |
∴实数a的取值集合是{0,-1,-
| 1 |
| 2 |
故选:D.
点评:本题考查实数a的求法,解题时要认真审题,是基础题.

练习册系列答案
相关题目
“x=1”是“x2-1=0”的( )
| A、充要条件 |
| B、必要不充分条件 |
| C、既非充分也非必要条件 |
| D、充分不必要条件 |
不等式x2-3x+2>0的解集为( )
| A、(-∞,-2)∪(-1,+∞) |
| B、(-∞,1)∪(2,+∞) |
| C、(-2,-1) |
| D、(1,2) |
过点A(1,0)和点B(m,4)的直线与直线y=2x+1平行,则m等于( )
| A、3 | B、5 | C、7 | D、9 |
 已知an=(
已知an=(| 1 |
| 3 |
A、(
| ||
B、(
| ||
C、(
| ||
D、(
|
圆
,(θ为参数)的圆心到直线
,(t为参数)的距离是( )
|
|
| A、1 | ||
B、
| ||
C、
| ||
| D、3 |
 如图,有一菱形纸片ABCD,∠A=60°,E是AD边上的一点(不包括A,D),先将ABCD沿对角线BD折成直二面角,再将△ABE沿BE翻折到△A′BE,下列不可能正确的是( )
如图,有一菱形纸片ABCD,∠A=60°,E是AD边上的一点(不包括A,D),先将ABCD沿对角线BD折成直二面角,再将△ABE沿BE翻折到△A′BE,下列不可能正确的是( )| A、BC与平面A′BE内某直线平行 |
| B、BC与平面A′BE内某直线垂直 |
| C、CD∥平面A′BE |
| D、CD⊥平面A′BE |
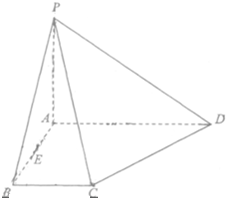 如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,且∠ABC=90°,AD∥BC,AD=2,AB=BC=1,PA⊥平面ABCD,E是线段AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,且∠ABC=90°,AD∥BC,AD=2,AB=BC=1,PA⊥平面ABCD,E是线段AB的中点.