题目内容
已知平面α外一点P,PA⊥α,A为垂足,B,C均在平面α内,∠BAC=120°,PA=AB,求PB与AC所成角的大小.
考点:异面直线及其所成的角
专题:空间角
分析:如图所示,设<
,
>=θ.不妨设PA=AB=AC=1,由∠BAC=120°,可得BC=
.由PA⊥α,可得
•
=0.|
|=
.利用数量积运算可得:
•
=-
2=-1,
•
=
×1×cosθ=
cosθ.根据
=
+
+
,利用数量积运算性质即可得出.
| BP |
| AC |
| 3 |
| PA |
| AC |
| PB |
| 2 |
| BP |
| PA |
| PA |
| BP |
| AC |
| 2 |
| 2 |
| BC |
| BP |
| PA |
| AC |
解答:
解:如图所示,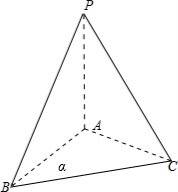
设<
,
>=θ.
不妨设PA=AB=AC=1,
∵∠BAC=120°,
∴BC=
.
∵PA⊥α,
∴
•
=0.|
|=
.
•
=-
2=-1,
•
=
×1×cosθ=
cosθ.
∵
=
+
+
,
∴
2=
2+
2+
2+2
•
+2
•
+2
•
.
∴3=2+1+1-2+2
cosθ+0,
化为cosθ=
.
∴PB与AC所成角的大小为arccos
.

设<
| BP |
| AC |
不妨设PA=AB=AC=1,
∵∠BAC=120°,
∴BC=
| 3 |
∵PA⊥α,
∴
| PA |
| AC |
| PB |
| 2 |
| BP |
| PA |
| PA |
| BP |
| AC |
| 2 |
| 2 |
∵
| BC |
| BP |
| PA |
| AC |
∴
| BC |
| BP |
| PA |
| AC |
| BP |
| PA |
| BP |
| AC |
| PA |
| AC |
∴3=2+1+1-2+2
| 2 |
化为cosθ=
| ||
| 4 |
∴PB与AC所成角的大小为arccos
| ||
| 4 |
点评:本题考查了利用数量积运算求空间角、线面垂直的性质,考查了推理能力和计算能力,属于中档题.

练习册系列答案
相关题目
若f(x)=x2-4ax+a2-1在(-∞,2)上是减函数,则a的取值范围是( )
| A、a≥1 | B、a<1 |
| C、a>1 | D、a≤1 |
在△ABC中,已知a=11,b=20,A=130°,则此三角形( )
| A、无解 | B、只有一解 |
| C、有两解 | D、解的个数不定 |
在区间[0,1]上任取两个数a、b,则方程x2+ax+b2=0有实根的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,已知a=4,b=6,C=120°,则边c的值是( )
| A、8 | ||
B、2
| ||
C、6
| ||
D、2
|
 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DBA=30°,∠DAB=60°,AD=1,PD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DBA=30°,∠DAB=60°,AD=1,PD⊥底面ABCD.