题目内容
在区间[0,1]上任取两个数a、b,则方程x2+ax+b2=0有实根的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:本题是一个等可能事件的概率,试验发生包含的事件是在区间[0,1]上任取两个数a和b,写出事件对应的集合,做出面积,满足条件的事件是关于x的方程x2+ax+b2=0有实数根,根据二次方程的判别式写出a,b要满足的条件,写出对应的集合,做出面积,得到概率.
解答:
解:由题意知本题是一个等可能事件的概率,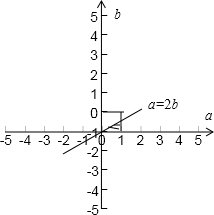
∵试验发生包含的事件是在区间[0,1]上任取两个数a和b,
事件对应的集合是Ω={(a,b)|0≤a≤1,0≤b≤1}
对应的面积是sΩ=1
满足条件的事件是关于x的方程x2+2ax+b2=0有实数根,
即a2-4b2≥0,
∴a≥2b,
事件对应的集合是A={(a,b)|0≤a≤1,0≤b≤1,a≥2b}
对应的图形的面积是sA=
×
×1=
,
∴根据等可能事件的概率得到P=
,
故选:B

∵试验发生包含的事件是在区间[0,1]上任取两个数a和b,
事件对应的集合是Ω={(a,b)|0≤a≤1,0≤b≤1}
对应的面积是sΩ=1
满足条件的事件是关于x的方程x2+2ax+b2=0有实数根,
即a2-4b2≥0,
∴a≥2b,
事件对应的集合是A={(a,b)|0≤a≤1,0≤b≤1,a≥2b}
对应的图形的面积是sA=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
∴根据等可能事件的概率得到P=
| 1 |
| 4 |
故选:B
点评:本题考查几何概型,古典概型和几何概型是我们学习的两大概型,古典概型要求能够列举出所有事件和发生事件的个数,而不能列举的就是几何概型,几何概型的概率的值是通过长度、面积、和体积、的比值得到.

练习册系列答案
相关题目
某产品计划每年成本降低p%,若三年后成本为a元,则现在成本为( )
| A、a(1+p%)元 | ||
| B、a(1-p%)元 | ||
C、
| ||
D、
|
函数f(x)=lnx-
(x-
)的零点个数是( )
| 1 |
| 2 |
| 1 |
| x |
| A、0 | B、1 | C、2 | D、3 |
设A,B,C,D是空间四个不同的点,在下列命题中,不正确的是( )
| A、若AC与BD共面,则AD与BC共面 |
| B、若AB=AC,DB=DC,则AD⊥BC |
| C、若AB=AC,DB=DC,则AD=BC |
| D、若AC与BD是异面直线,则AD与BC也是异面直线 |
两个二进制数101(2)与110(2)的和用十进制数表示为( )
| A、12 | B、11 | C、10 | D、9 |
若a∈R,则a=0是a(a-1)=0的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,边长为2,∠BCD=60°,点E为PB的中点,四边形ABCD的两对角线交点为F.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,边长为2,∠BCD=60°,点E为PB的中点,四边形ABCD的两对角线交点为F.