题目内容
19.设函数$f(x)=\sqrt{3}sinxcosx-{cos^2}x-\frac{1}{2},x∈R$.(I)求函数f(x)的最小正周期;
(Ⅱ)若$x∈({0,\frac{π}{2}})$,求函数f(x)的值域.
分析 (1)利用倍角公式及两角差的正弦函数公式化简可得解析式:f(x)=sin(2x-$\frac{π}{6}$)-1,利用周期公式即可得解;
(2)由$x∈({0,\frac{π}{2}})$,可得2x-$\frac{π}{6}$∈(-$\frac{π}{6}$,$\frac{5π}{6}$),利用正弦函数的图象和性质即可求得其值域.
解答 解:(1)∵$f(x)=\sqrt{3}sinxcosx-{cos^2}x-\frac{1}{2},x∈R$.
=$\frac{\sqrt{3}}{2}$sin2x-$\frac{cos2x+1}{2}$-$\frac{1}{2}$
=sin(2x-$\frac{π}{6}$)-1,
∴T=$\frac{2π}{2}=π$.
(2)∵$x∈({0,\frac{π}{2}})$,
∴2x-$\frac{π}{6}$∈(-$\frac{π}{6}$,$\frac{5π}{6}$),
∴sin(2x-$\frac{π}{6}$)∈(-$\frac{1}{2}$,1],
∴f(x)∈(-$\frac{3}{2}$,0].
点评 本题主要考查了倍角公式及两角差的正弦函数公式,周期公式,正弦函数的图象和性质的综合应用,考查了计算能力,属于基础题.

练习册系列答案
相关题目
9.一个几何体的三视图如图所示,则这个几何体的外接球的体积为( )
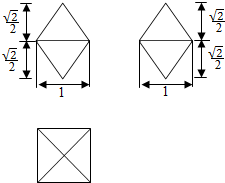

| A. | $\frac{{\sqrt{2}}}{3}π$? | B. | $\sqrt{2}π$? | C. | 2π? | D. | $\frac{{2\sqrt{2}}}{3}π$? |
10.条件p:|x+1|>1,条件$q:\frac{1}{3-x}>1$,则¬q是¬p的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
14.若函数f(x)=ax-1+1(a>0且a≠1)的反函数恒过定点( )
| A. | (0,2) | B. | (2,0) | C. | (1,2) | D. | (2,1) |
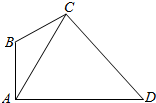 在如图所示的四边形ABCD中,已知AB⊥AD,∠ABC=120°,∠ACD=60°,AD=2$\sqrt{3}$,设∠ACB=θ,点C到AD的距离为h.
在如图所示的四边形ABCD中,已知AB⊥AD,∠ABC=120°,∠ACD=60°,AD=2$\sqrt{3}$,设∠ACB=θ,点C到AD的距离为h.