题目内容
4.△ABC中,点A(4,-1),AB的中点为M(3,2),重心为P(4,2),求边BC的长.分析 根据题意,画出图形,结合图形,利用AB的中点坐标求出点B的坐标,
再利用重心坐标求出BC边的中点N的坐标,即可求出边长BC的值.
解答 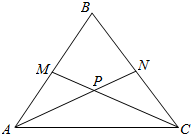 解:△ABC中,点A(4,-1),AB的中点为M(3,2),重心为P(4,2),
解:△ABC中,点A(4,-1),AB的中点为M(3,2),重心为P(4,2),
画出图形,如图所示;
设点B的坐标为(x,y),则
$\left\{\begin{array}{l}{\frac{x+4}{2}=3}\\{\frac{y-1}{2}=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=5}\end{array}\right.$,即B(2,5);
延长AP交BC与点N,则$\overrightarrow{AP}$=2$\overrightarrow{PN}$,
设点N的坐标为(x′,y′),
则$\overrightarrow{AP}$=(0,3),$\overrightarrow{PN}$=(x′-4,y′-2);
∴$\left\{\begin{array}{l}{2(x′-4)=0}\\{2(y′-2)=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x′=4}\\{y′=\frac{7}{2}}\end{array}\right.$,
∴点N(4,$\frac{7}{2}$),
∴BN=$\sqrt{{(4-2)}^{2}{+(\frac{7}{2}-5)}^{2}}$=$\frac{5}{2}$,
∴边长BC=2BN=5.
点评 本题考查了直线方程的应用问题,也考查了三角形的重心与线段中点的应用问题,是综合性题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目