题目内容

10．已知复数$\frac{4i}{1+i}$，则它在复平面内对应的点应该在（　　）
A．第一象限B．第二象限C．第三象限D．第四象限

分析 直接利用复数代数形式的乘除运算化简复数$\frac{4i}{1+i}$，求出它在复平面内对应的点的坐标，则答案可求．

解答 解：$\frac{4i}{1+i}$=$\frac{4i（1-i）}{（1+i）（1-i）}=2i-2{i}^{2}=2+2i$，
则它在复平面内对应的点的坐标为：（2，2），位于第一象限．
故选：A．

点评 本题考查了复数代数形式的乘除运算，考查了复数的代数表示法及其几何意义，是基础题．

练习册系列答案
相关题目
20．等差数列{an}中，a3+a5=16，则a4=（　　）
A．8B．6C．4D．2
1．已知平面向量$\overrightarrow a$=（2，-1），向上平移2个单位，再向左平移1个单位得到向量$\overrightarrow{b}$，则$\overrightarrow{b}$=（1，1）．
18．若复数z1=a+2i（a∈R），z2=3-4i，且$\frac{{z}_{1}}{{z}_{2}}$为纯虚数，则|z1|=$\frac{10}{3}$．
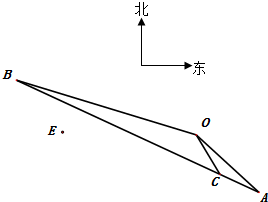5．如图，某自行车手从O点出发，沿折线O-A-B-O匀速骑行，其中点A位于点O南偏东45°且与点O相距20$\sqrt{2}$千米．该车手于上午8点整到达点A，8点20分骑至点C，其中点C位于点O南偏东（45°-α）（其中sinα=$\frac{1}{{\sqrt{26}}}$，0°＜α＜90°）且与点O相距5$\sqrt{13}$千米（假设所有路面及观测点都在同一水平面上）．
（1）求该自行车手的骑行速度；
（2）若点O正西方向27.5千米处有个气象观测站E，假定以点E为中心的3.5千米范围内有长时间的持续强降雨．试问：该自行车手会不会进入降雨区，并说明理由．
15．在平面直角坐标系xOy中，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{{\sqrt{3}}}{2}$，且点（$\sqrt{3}$，$\frac{1}{2}$）在椭圆C上．
（1）求椭圆C的方程；
（2）设椭圆E：$\frac{{x}^{2}}{4{a}^{2}}$+$\frac{{y}^{2}}{4{b}^{2}}$=1，P为椭圆C上任意一点，过点P的直线y=kx+m交椭圆E于A，B两点，射线PO交椭圆E于点Q．
（i）求证$\frac{|OQ|}{|OP|}$=2；
（ii）求△ABQ面积的最大值．
2．在空间直角坐标系中，若A（2，-2，1），B（4，2，3），C（x，y，2）三点共线，则$\left|\overrightarrow{BC}\right|$=（　　）
A．$\sqrt{6}$B．$2\sqrt{6}$C．$\sqrt{5}$D．$2\sqrt{5}$
19．若函数f（x）=lg（8+2x-x2）的定义域为M，函数g（x）=$\sqrt{1-\frac{2}{x-1}}$的定义域为N，求集合M，N，M∩N．
20．若（1+x）4=a0+a1x+a2x2+a3x3+a4x4，则a1+a2+a3+a4的值为（　　）
A．0B．15C．16D．17

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网