��Ŀ����
5��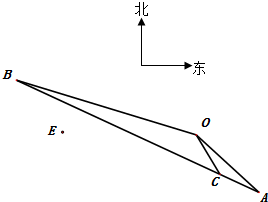 ��ͼ��ij���г��ִ�O�������������O-A-B-O�������У����е�Aλ�ڵ�O��ƫ��45�������O���20$\sqrt{2}$ǧ�ף��ó���������8���������A��8��20��������C�����е�Cλ�ڵ�O��ƫ����45��-����������sin��=$\frac{1}{{\sqrt{26}}}$��0�㣼����90�㣩�����O���5$\sqrt{13}$ǧ�ף���������·�漰�۲�㶼��ͬһˮƽ���ϣ���
��ͼ��ij���г��ִ�O�������������O-A-B-O�������У����е�Aλ�ڵ�O��ƫ��45�������O���20$\sqrt{2}$ǧ�ף��ó���������8���������A��8��20��������C�����е�Cλ�ڵ�O��ƫ����45��-����������sin��=$\frac{1}{{\sqrt{26}}}$��0�㣼����90�㣩�����O���5$\sqrt{13}$ǧ�ף���������·�漰�۲�㶼��ͬһˮƽ���ϣ�����1��������г��ֵ������ٶȣ�
��2������O��������27.5ǧ�״��и�����۲�վE���ٶ��Ե�EΪ���ĵ�3.5ǧ��Χ���г�ʱ��ij���ǿ���꣮���ʣ������г��ֻ����뽵��������˵�����ɣ�
���� ��1���������Ҷ������������AC�ij�������������г����ٶȣ�
��2���ȸ������Ҷ������������cos��OAC���ٸ������Ҷ����ɵ�OM������Rt��EHM�У����EM�Ĵ�С���Ƚϼ��ɣ�
���  �⣺��1�������⣬֪��OA=20$\sqrt{2}$��OC=5 $\sqrt{13}$��
�⣺��1�������⣬֪��OA=20$\sqrt{2}$��OC=5 $\sqrt{13}$��
��AOC=����sin��=$\frac{1}{\sqrt{26}}$��
����0�㣼����90�㣬����cos=$\sqrt{1-��\frac{1}{\sqrt{26}}}��^{2}$=$\frac{5\sqrt{26}}{26}$��
�����Ҷ�������AC=$\sqrt{O{A}^{2}+O{C}^{2}-2OA•OC•cos��}$=5$\sqrt{5}$��
���Ը����г��ֵ���ʻ�ٶ�Ϊ$\frac{5\sqrt{5}}{\frac{1}{3}}$=15$\sqrt{5}$ ��ǧ��/Сʱ����
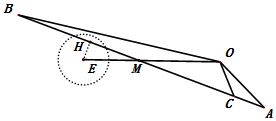
��2����ͼ����ֱ��OE��AB�ཻ�ڵ�M���ڡ�AOC�У������Ҷ�����
�ã�cos��OAC=$\frac{O{A}^{2}+A{C}^{2}-O{C}^{2}}{2OC•AC}$=$\frac{2{0}^{2}��2+{5}^{2}��5-{5}^{2}��13}{2��20\sqrt{2}��5\sqrt{5}}$=$\frac{3\sqrt{10}}{10}$��
�Ӷ� sin��OAC=$\sqrt{1-\frac{9}{10}}$=$\frac{\sqrt{10}}{10}$��
�ڡ�AOM�У������Ҷ������ã�OM=$\frac{OAsin��OAM}{sin��45��-��OAM��}$=$\frac{20\sqrt{2}��\frac{\sqrt{10}}{10}}{\frac{\sqrt{2}}{2}��\frac{3\sqrt{10}}{10}-\frac{\sqrt{10}}{10}��}$=20��
����OE=27.5��40=OM�����Ե�Mλ�ڵ�O�͵�E֮�䣬��ME=OE-OM=7.5��
����E��EH AB�ڵ�H����EHΪ��E��ֱ��AB�ľ��룮
��Rt��EHM�У�EH=EM•sin��EMH=EM•sin��45��-��OAC��=7.5��$\frac{\sqrt{5}}{5}$=$\frac{3\sqrt{5}}{2}$��3.5��
���Ը����г��ֻ���뽵������
���� ���⿼�������Ҷ��������Ҷ����Լ��������ε��й�֪ʶ�������е��⣮

 ����ͼ���������������ϵ�д�
����ͼ���������������ϵ�д� ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�| A�� | -6��1-3-8�� | B�� | $\frac{1}{9}��1-{3^{-8}}��$ | C�� | 3��1-3-8�� | D�� | 3��1+3-8�� |
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |