题目内容
19.到两定点(-2,0),(2,0)的距离之差的绝对值为定值3的点的轨迹是( )| A. | 椭圆 | B. | 线段 | C. | 直线 | D. | 双曲线 |
分析 根据题意,求出两个定点之间的距离为4,比较可得其大于到这两点的距离之差的绝对值,由双曲线的定义可得其轨迹为双曲线,即可得答案.
解答 解:根据题意,两定点为(-2,0),(2,0),
这两个定点之间的距离为4,
而4>3,
则要求的轨迹是以(-2,0),(2,0)为焦点的双曲线;
故选:D.
点评 本题考查双曲线的定义,注意比较两定点之间的距离与距离之差的绝对值之间的大小关系.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
7.等比数列{an}中,a3=9,前3项和为${S_3}=3\int_0^3{x^2}dx$,则公比q的值是( )
| A. | 1 | B. | $-\frac{1}{2}$ | C. | 1或$-\frac{1}{2}$ | D. | -1或$-\frac{1}{2}$ |
8.已知正四面体ABCD的棱长为a,点E,F,H分别是BC,AD,AE的中点,则$\overrightarrow{AH}•\overrightarrow{AF}$的值为( )
| A. | $\frac{1}{2}{a^2}$ | B. | $\frac{1}{4}{a^2}$ | C. | $\frac{1}{8}{a^2}$ | D. | $\frac{{\sqrt{3}}}{8}{a^2}$ |
9.下列函数既是奇函数,又在区间(0,+∞)上是增函数的是( )
| A. | y=x-1 | B. | y=x2 | C. | y=lgx | D. | y=x3 |
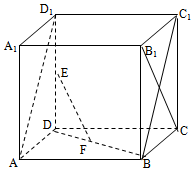 如图,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、BD的中点.
如图,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、BD的中点.