题目内容
用单调性定义证明函数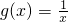 在(0,+∞)上单调递减.
在(0,+∞)上单调递减.
证明:在(0,+∞)内任取x1,x2,令x1<x2,
f(x1)-f(x2)= =
= ,
,
∵0<x1<x2,
∴x2-x1>0,x1x2>0,
∴f(x1)-f(x2)= >0,
>0,
∴函数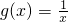 在(0,+∞)上单调递减.
在(0,+∞)上单调递减.
分析:在在(0,+∞)内任取x1,x2,令x1<x2,推导出f(x1)-f(x2)= >0,由此能够证明函数
>0,由此能够证明函数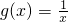 在(0,+∞)上单调递减.
在(0,+∞)上单调递减.
点评:本题考查利用定义法证明函数的单调性,是基础题.解题时要认真审题,仔细解答.
f(x1)-f(x2)=
 =
= ,
,∵0<x1<x2,
∴x2-x1>0,x1x2>0,
∴f(x1)-f(x2)=
 >0,
>0,∴函数
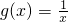 在(0,+∞)上单调递减.
在(0,+∞)上单调递减.分析:在在(0,+∞)内任取x1,x2,令x1<x2,推导出f(x1)-f(x2)=
 >0,由此能够证明函数
>0,由此能够证明函数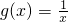 在(0,+∞)上单调递减.
在(0,+∞)上单调递减.点评:本题考查利用定义法证明函数的单调性,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 设f(x)=
设f(x)=