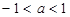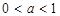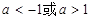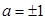题目内容
如图,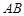 是圆
是圆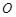 的直径,
的直径,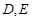 为圆上位于
为圆上位于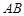
异侧的两点,连结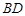 并延长至点
并延长至点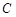 ,使
,使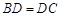 ,连结
,连结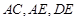 .
.
求证: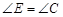 .
.
 是圆
是圆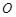 的直径,
的直径,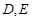 为圆上位于
为圆上位于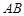
异侧的两点,连结
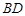 并延长至点
并延长至点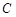 ,使
,使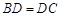 ,连结
,连结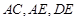 .
.求证:
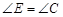 .
.
见解析
【考点】圆周角定理,线段垂直平分线的判定和性质,等腰三角形的性质。
【考点】圆周角定理,线段垂直平分线的判定和性质,等腰三角形的性质。
要证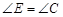 ,就得找一个中间量代换,一方面考虑到
,就得找一个中间量代换,一方面考虑到 是同弧所对圆周角,相等;另
是同弧所对圆周角,相等;另
一方面由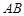 是圆
是圆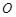 的直径和
的直径和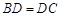 可知
可知 是线段
是线段 的中垂线,从而根据线段中垂线上的点到线段两端的距离相等和等腰三角形等边对等角的性质得到
的中垂线,从而根据线段中垂线上的点到线段两端的距离相等和等腰三角形等边对等角的性质得到 。从而得证。
。从而得证。
本题还可连接 ,利用三角形中位线来求证
,利用三角形中位线来求证
证明:连接 。
。

∵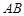 是圆
是圆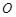 的直径,∴
的直径,∴ (直径所对的圆周角是直角)。
(直径所对的圆周角是直角)。
∴ (垂直的定义)。
(垂直的定义)。
又∵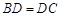 ,∴
,∴ 是线段
是线段 的中垂线(线段的中垂线定义)。
的中垂线(线段的中垂线定义)。
∴ (线段中垂线上的点到线段两端的距离相等)。
(线段中垂线上的点到线段两端的距离相等)。
∴ (等腰三角形等边对等角的性质)。
(等腰三角形等边对等角的性质)。
又∵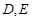 为圆上位于
为圆上位于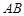 异侧的两点,
异侧的两点,
∴ (同弧所对圆周角相等)。
(同弧所对圆周角相等)。
∴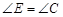 (等量代换)。
(等量代换)。
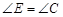 ,就得找一个中间量代换,一方面考虑到
,就得找一个中间量代换,一方面考虑到 是同弧所对圆周角,相等;另
是同弧所对圆周角,相等;另一方面由
 是圆
是圆 的直径和
的直径和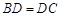 可知
可知 是线段
是线段 的中垂线,从而根据线段中垂线上的点到线段两端的距离相等和等腰三角形等边对等角的性质得到
的中垂线,从而根据线段中垂线上的点到线段两端的距离相等和等腰三角形等边对等角的性质得到 。从而得证。
。从而得证。本题还可连接
 ,利用三角形中位线来求证
,利用三角形中位线来求证
证明:连接
 。
。
∵
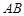 是圆
是圆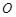 的直径,∴
的直径,∴ (直径所对的圆周角是直角)。
(直径所对的圆周角是直角)。∴
 (垂直的定义)。
(垂直的定义)。又∵
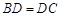 ,∴
,∴ 是线段
是线段 的中垂线(线段的中垂线定义)。
的中垂线(线段的中垂线定义)。∴
 (线段中垂线上的点到线段两端的距离相等)。
(线段中垂线上的点到线段两端的距离相等)。∴
 (等腰三角形等边对等角的性质)。
(等腰三角形等边对等角的性质)。又∵
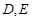 为圆上位于
为圆上位于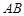 异侧的两点,
异侧的两点,∴
 (同弧所对圆周角相等)。
(同弧所对圆周角相等)。∴
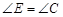 (等量代换)。
(等量代换)。
练习册系列答案
相关题目
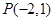 且被圆C:
且被圆C: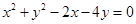 截得弦最长的直线l的方程是( )
截得弦最长的直线l的方程是( ) 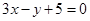
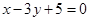
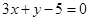
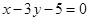
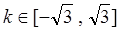 ,直线
,直线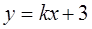 与圆
与圆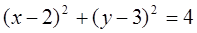 相交于M、N两点,则|MN|
相交于M、N两点,则|MN|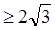 的概率为
的概率为 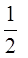
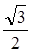
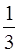
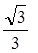
 中,圆
中,圆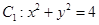 ,圆
,圆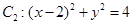 。
。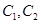 的极坐标方程,并求出圆
的极坐标方程,并求出圆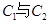 的公共弦的参数方程。
的公共弦的参数方程。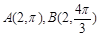 ,C是曲线
,C是曲线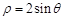 上任意一点,则
上任意一点,则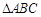 的面积的最小值等于 .
的面积的最小值等于 .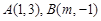 ,直线
,直线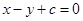 将这两圆的面积均平分,则
将这两圆的面积均平分,则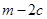 的值是( )
的值是( )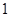
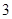
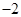
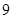
 与圆
与圆 交于
交于 、
、 两点,且
两点,且 对称,则弦
对称,则弦 的长为
的长为 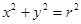 与直线
与直线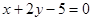 相交于
相交于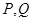 两点, 若
两点, 若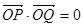 (
(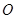 为原点),则圆的半径
为原点),则圆的半径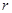 值的为 ;
值的为 ; 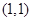 在圆
在圆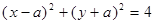 的内部,则
的内部,则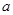 的取值范围是
的取值范围是