题目内容
在直角坐标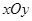 中,圆
中,圆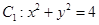 ,圆
,圆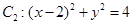 。
。
(Ⅰ)在以O为极点,x轴正半轴为极轴的极坐标系中,分别写出圆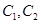 的极坐标方程,并求出圆
的极坐标方程,并求出圆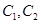 的交点坐标(用极坐标表示);
的交点坐标(用极坐标表示);
(Ⅱ)求圆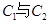 的公共弦的参数方程。
的公共弦的参数方程。
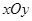 中,圆
中,圆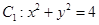 ,圆
,圆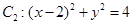 。
。(Ⅰ)在以O为极点,x轴正半轴为极轴的极坐标系中,分别写出圆
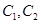 的极坐标方程,并求出圆
的极坐标方程,并求出圆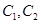 的交点坐标(用极坐标表示);
的交点坐标(用极坐标表示);(Ⅱ)求圆
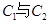 的公共弦的参数方程。
的公共弦的参数方程。(1) (2)
(2)  ,
, .
.
 (2)
(2)  ,
, .
.(Ⅰ)圆 的极坐标方程为
的极坐标方程为 ,
,
圆 的极坐标方程为
的极坐标方程为 .
.
解 得
得 ,
, ,
,
故圆 与圆
与圆 交点的坐标为
交点的坐标为 .
.
注:极坐标系下点的表示不唯一.
(Ⅱ)(解法一)
由 得圆
得圆 与圆
与圆 交点的直角坐标分别为
交点的直角坐标分别为 .
.
故圆 与圆
与圆 的公共弦的参数方程为
的公共弦的参数方程为
 .
.
(或参数方程写成 ,
, )
)
(解法二)
将x=1代入 ,得
,得 ,
,
从而 .
.
于是圆 与圆
与圆 的公共弦的参数方程为
的公共弦的参数方程为 ,
, .
.
考点定位:本大题主要考查直角坐标系与极坐标系之间的互化,意在考查考生利用坐标之间的转化求解。
 的极坐标方程为
的极坐标方程为 ,
,圆
 的极坐标方程为
的极坐标方程为 .
.解
 得
得 ,
, ,
,故圆
 与圆
与圆 交点的坐标为
交点的坐标为 .
.注:极坐标系下点的表示不唯一.
(Ⅱ)(解法一)
由
 得圆
得圆 与圆
与圆 交点的直角坐标分别为
交点的直角坐标分别为 .
.故圆
 与圆
与圆 的公共弦的参数方程为
的公共弦的参数方程为
 .
.(或参数方程写成
 ,
, )
)(解法二)
将x=1代入
 ,得
,得 ,
,从而
 .
.于是圆
 与圆
与圆 的公共弦的参数方程为
的公共弦的参数方程为 ,
, .
.考点定位:本大题主要考查直角坐标系与极坐标系之间的互化,意在考查考生利用坐标之间的转化求解。

练习册系列答案
相关题目
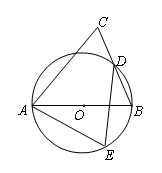
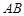 是圆
是圆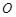 的直径,
的直径,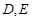 为圆上位于
为圆上位于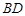 并延长至点
并延长至点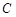 ,使
,使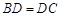 ,连结
,连结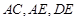 .
.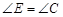 .
.
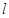 与圆
与圆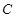 相交于点
相交于点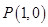 和点
和点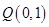 。
。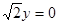 ,经过椭圆
,经过椭圆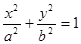 (a>b>0)的右焦点F及上顶点B,过椭圆外一点M(m,0)(m>0)的倾斜角为
(a>b>0)的右焦点F及上顶点B,过椭圆外一点M(m,0)(m>0)的倾斜角为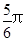 的直线l交椭圆于C、D两点.
的直线l交椭圆于C、D两点.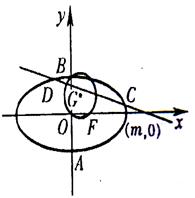
 且与圆
且与圆 相切的直线与两坐标轴围成的三角形的面积为 。
相切的直线与两坐标轴围成的三角形的面积为 。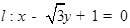 ,一个圆的圆心
,一个圆的圆心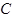 在
在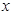 轴正半轴上,且该圆与直线
轴正半轴上,且该圆与直线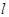 和
和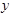 轴均相切.
轴均相切.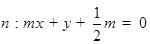 与圆
与圆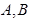 两点,且
两点,且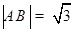 ,求
,求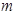 的值.
的值. 关于直线
关于直线
 对称,则
对称,则 的取值范围是( )
的取值范围是( ) ]
] 以原点为圆心,且与圆
以原点为圆心,且与圆 外切.
外切. 与圆
与圆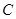 相交;
相交;