题目内容
【题目】已知![]() ,其中
,其中![]() 是实常数.
是实常数.
(1)若![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若![]() ,求证:函数
,求证:函数![]() 的零点有且仅有一个;
的零点有且仅有一个;
(3)若![]() ,设函数
,设函数![]() 的反函数为
的反函数为![]() ,若
,若![]() 是公差
是公差![]() 的等差数列且均在函数
的等差数列且均在函数![]() 的值域中,求证:
的值域中,求证:![]() .
.
【答案】(1)![]() (2)证明见解析;(3)证明见解析;
(2)证明见解析;(3)证明见解析;
【解析】
(1)直接解不等式![]() 即可;
即可;
(2)说明函数是增函数,然后由![]() ,
,![]() 可得结论;
可得结论;
(3)首先不等式变形:![]() ,即
,即
![]() ,而
,而![]() ,问题转化为证明
,问题转化为证明![]() 是关于
是关于![]() 的减函数,即设
的减函数,即设![]() ,证明
,证明![]() ,利用反函数定义,设
,利用反函数定义,设![]() ,由
,由![]() 单调递增可得
单调递增可得![]() 之间的大小关系,得
之间的大小关系,得![]() .
.
作两个差![]() ,
,![]() ,并相减得
,并相减得![]() ,若
,若![]() ,此式中分析左右两边出现矛盾,从而只能有
,此式中分析左右两边出现矛盾,从而只能有![]() ,证得结论.
,证得结论.
(1)![]() ,所以
,所以![]() ,
,![]() ,易知
,易知![]() ,所以
,所以![]() ,所以
,所以![]() .
.
(2)函数![]() 为增函数,且
为增函数,且![]() ,由于
,由于![]() .故在
.故在![]() 上必存在
上必存在![]() ,使
,使![]() .又
.又![]() 为增函数,所以函数
为增函数,所以函数![]() 的零点有且仅有一个.
的零点有且仅有一个.
(3)即证:![]() .
.
![]() ,而
,而![]() ,所以只需证
,所以只需证![]() 是关于
是关于![]() 的减函数.
的减函数.
设![]() ,即证
,即证![]() ※大于0
※大于0
设![]() ,由
,由![]() 单调递增可得
单调递增可得![]() .
.
![]() .
.
而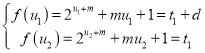 ,
,
两式相减得![]() ,
,
![]() ①
①
同理![]() ②,
②,
①-②得:
![]() .
.
若![]() ,则上式左侧
,则上式左侧![]() ,右侧
,右侧![]() 矛盾,故※
矛盾,故※![]() .证毕.
.证毕.

练习册系列答案
相关题目