题目内容
7.函数f(x)=x2+2x+2的最小值是( )| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
分析 运用配方,可得f(x)=x2+2x+2=(x+1)2+1,即可得到最小值.
解答 解:函数f(x)=x2+2x+2=(x+1)2+1,
当x=-1时,f(x)的最小值为1.
故选:C.
点评 本题考查二次函数的最值的求法,注意运用配方法,考查运算能力,属于基础题.

练习册系列答案
相关题目
15.请观察数列:1,1,2,3,5,( ),13…运用合情推理,括号里的数最可能是( )
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
2.曲线C:$\frac{x^2}{4-k}+\frac{y^2}{k-1}$=1表示双曲线,则k的取值范围为( )
| A. | 1<k<4 | B. | k>4 | C. | k<0 | D. | k<1或k>4 |
19.f(x)=$\frac{-{x}^{2}+x+k}{{e}^{x}}$有极值,则k的取值范围是( )
| A. | k≥$\frac{5}{4}$ | B. | k>-$\frac{5}{4}$ | C. | k≤-$\frac{5}{4}$ | D. | k<-$\frac{5}{4}$ |
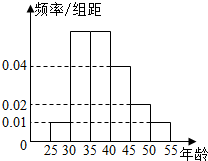 为响应工业园区举行的万人体质监测活动,某高校招募了N名志愿服务者,将所有志愿者按年龄情况分为25~30,30~35,35~40,45~50,50~55六个层次,其频率分布直方图如图所示,已知35~45之间的志愿者共20人.
为响应工业园区举行的万人体质监测活动,某高校招募了N名志愿服务者,将所有志愿者按年龄情况分为25~30,30~35,35~40,45~50,50~55六个层次,其频率分布直方图如图所示,已知35~45之间的志愿者共20人.