题目内容
7.已知F1、F2为椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1的左、右焦点,过F1且垂直于F1F2的直线交椭圆于A,B两点,则线段AB的长是$\frac{9}{2}$.分析 由椭圆的标准方程可得c,把x=-c代入椭圆的标准方程解出y即可得出.
解答 解:∵c2=16-9=7,∴c=$\sqrt{7}$,可得F1$(-\sqrt{7},0)$.
将x=-$\sqrt{7}$代入椭圆方程$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1中,得到$\frac{7}{16}+\frac{{y}^{2}}{9}$=1,解得y=$±\frac{9}{4}$.
所以线段AB的长是2×$\frac{9}{4}$=$\frac{9}{2}$.
故答案为:$\frac{9}{2}$.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交弦长问题,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
17.某港口水的深度y(m)是时间t(0≤t≤24,单位:h)的函数,记作y=f(t).下面是某日水深的数据:
经长期观察,y=f(t)的曲线可以近似地看成函数y=Asinωt+b的图象.一般情况下,船舶航行时,船底离海底的距离为5m或5m以上时认为是安全的(船舶停靠时,船底只需不碰海底即可).某船吃水程度(船底离水面的距离)为6.5m,如果该船希望在同一天内安全进出港,请问,它最多能在港内停留( )小时(忽略进出港所需的时间).
| t/h | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y/m | 10 | 13 | 10 | 7 | 10 | 13 | 10 | 7 | 10 |
| A. | 6 | B. | 12 | C. | 16 | D. | 18 |
15.在直三棱柱ABC-A1B1C1中,AB=BC=1,AC=$\sqrt{2}$,BB1=2,点M为BB1的中点,则点A到平面A1CM距离为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{3\sqrt{2}}{2}$ |
2.运行下列程序,若输入的p,q的值分别为70,30,则输出的p-q的值为( )


| A. | 47 | B. | 54 | C. | 61 | D. | 68 |
16.若复数$z=\frac{1+i}{1-i}$,$\overline z$为z的共轭复数,则${({\overline z})^{2017}}$=( )
| A. | i | B. | -i | C. | -22017i | D. | 22017i |
 一个空间几何体的三视图(单位:cm)如图所示,则该几何体的表面积为30+6$\sqrt{5}$cm2.
一个空间几何体的三视图(单位:cm)如图所示,则该几何体的表面积为30+6$\sqrt{5}$cm2.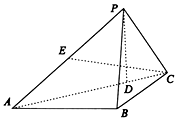 如图,在三棱锥P-ABC中,PA⊥PC,PB=AB=BC=2,∠ABC=120°,$PC=\sqrt{3}$,D为AC上一点,且AD=3DC.
如图,在三棱锥P-ABC中,PA⊥PC,PB=AB=BC=2,∠ABC=120°,$PC=\sqrt{3}$,D为AC上一点,且AD=3DC.