题目内容
已知角α的顶点与平面直角坐标系的原点重合,始边在x轴的非负半轴上,终边经过点P(-1,2),求sin(2α+
π)的值.
| 2 |
| 3 |
考点:两角和与差的正弦函数
专题:三角函数的求值
分析:由题意和三角函数定义可得sinα和cosα,再由二倍角公式可得sin2α和cos2α,代入sin(2α+
π)=sin2αcos
+cos2αsin
化简可得.
| 2 |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
解答:
解:由题意和三角函数的定义可得sinα=
,cosα=
,
∴sin2α=2sinαcosα=-
,cos2α=cos2α-sin2α=-
,
∴sin(2α+
π)=sin2αcos
+cos2αsin
=-
×(-
)+(-
)×
=
| 2 | ||
|
| -1 | ||
|
∴sin2α=2sinαcosα=-
| 4 |
| 5 |
| 3 |
| 5 |
∴sin(2α+
| 2 |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
=-
| 4 |
| 5 |
| 1 |
| 2 |
| 3 |
| 5 |
| ||
| 2 |
4-3
| ||
| 10 |
点评:本题考查两角和与差的正弦函数,涉及三角函数的定义和二倍角公式,属基础题.

练习册系列答案
相关题目
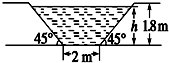 如图,某灌溉渠的横断面是等腰梯形,底宽为2m,渠深为1.8m,斜坡的倾斜角是45°.(临界状态不考虑)
如图,某灌溉渠的横断面是等腰梯形,底宽为2m,渠深为1.8m,斜坡的倾斜角是45°.(临界状态不考虑)