题目内容
20.已知圆x2+y2+2x-2y+2a=0截直线x+y+2=0所得弦长为4,则实数a的值是( )| A. | -1 | B. | -2 | C. | -3 | D. | -4 |
分析 把圆的方程化为标准形式,求出弦心距,再由条件根据弦长公式求得a的值.
解答 解:圆x2+y2+2x-2y+2a=0 即 (x+1)2+(y-1)2=2-2a,
故弦心距d=$\frac{|-1+1+2|}{\sqrt{2}}$=$\sqrt{2}$.
再由弦长公式可得 2-2a=2+4,∴a=-2
故选:B.
点评 本题主要考查直线和圆的位置关系,点到直线的距离公式,弦长公式的应用,属于基础题.

练习册系列答案
相关题目
12.给出下列命题:
①若a,b,m都是正数,且$\frac{a+m}{b+m}>\frac{a}{b}$,则a<b;
②若f'(x)是f(x)的导函数,若?x∈R,f'(x)≥0,则f(1)<f(2)一定成立;
③命题“?x∈R,x2-2x+1<0”的否定是真命题;
④“|x|≤1,且|y|≤1”是“|x+y|≤2”的充分不必要条件.
其中正确命题的序号是( )
①若a,b,m都是正数,且$\frac{a+m}{b+m}>\frac{a}{b}$,则a<b;
②若f'(x)是f(x)的导函数,若?x∈R,f'(x)≥0,则f(1)<f(2)一定成立;
③命题“?x∈R,x2-2x+1<0”的否定是真命题;
④“|x|≤1,且|y|≤1”是“|x+y|≤2”的充分不必要条件.
其中正确命题的序号是( )
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
9.设a=30.5,b=log32,c=cos$\frac{2π}{3}$,则( )
| A. | a<b<c | B. | c<a<b | C. | b<c<a | D. | c<b<a |
10.若z(1+i)=(1-i)2(i为虚数单位),则z=( )
| A. | 1+i | B. | 1-i | C. | -1+i | D. | -1-i |
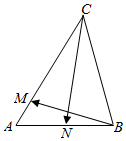 在△ABC中,AB=3,AC=4,N是AB的中点,M是边AC(含端点)上的动点.
在△ABC中,AB=3,AC=4,N是AB的中点,M是边AC(含端点)上的动点.