Question

如图，长方体ABCD-A₁B₁C₁D₁中，AB=AA₁=1，BC=

2

，M是AD中点，N是B₁C₁中点．
（Ⅰ）求证：NA₁∥CM；
（Ⅱ）求证：平面A₁MCN⊥平面A₁BD₁．

Answer 1

考点：平面与平面垂直的判定,空间中直线与直线之间的位置关系

专题：证明题,空间位置关系与距离

分析：（Ⅰ）以D为原点，建立空间直角坐标系D-xyz，求出

NA1

=（

2

2

，-1，0），

CM

=（

2

2

，-1，0），可得

NA1

=

CM

，即可证明NA₁∥CM；
（Ⅱ）证明

D1B

•

MN

=0+1-1=0，

D1B

•

CM

=0，即可证明D₁B⊥平面A₁MCN，从而平面A₁MCN⊥平面A₁BD₁．

解答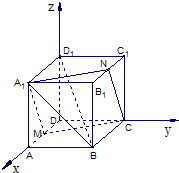： 证明：（Ⅰ）以D为原点，建立空间直角坐标系D-xyz，则B(

2

，1，0)，A(

2

，0，1)，D1(0，0，1)，C(0，1，0)，M(

2

2

，0，0)，N(

2

2

，1，1)
∴

NA1

=（

2

2

，-1，0），

CM

=（

2

2

，-1，0），
∴

NA1

=

CM

，
∴NA₁∥CM；
（Ⅱ）∵

D1B

=（

2

，1，-1），

MN

=（0，1，1），

CM

=（

2

2

，-1，0），
∴

D1B

•

MN

=0+1-1=0，

D1B

•

CM

=0，
∴D₁B⊥MN，D₁B⊥CM，
又MN∩CM=M，…（6分）
∴D₁B⊥平面A₁MCN，又D₁B?平面A₁BD₁，
∴平面A₁MCN⊥平面A₁BD₁．

点评：本题考查平面与平面垂直的判定，考查空间向量的运用，正确求出向量的坐标是关键．