题目内容
在△ABC中,BC=2,B=
,若△ABC的面积为
,求tanC的值.
| π |
| 3 |
| ||
| 2 |
考点:三角形的面积公式,余弦定理
专题:解三角形
分析:由BC=2,B=
,△ABC的面积为
,利用三角形面积计算公式可得BA=1.再利用余弦定理可得:b2=a2+c2-2accosB,可得b.利用勾股定理的逆定理判断出A=
.利用直角三角形的边角关系即可得出.
| π |
| 3 |
| ||
| 2 |
| π |
| 2 |
解答:
解:∵BC=2,B=
,△ABC的面积为
,
∴
×2×BA•sin
=
,解得BA=1.
由余弦定理可得:b2=a2+c2-2accosB=22+12-2×2×1×
=3,
∴b=
.
∵a2=b2+c2,
∴A=
.
又a=2c,
∴C=
.
∴tanC=
.
| π |
| 3 |
| ||
| 2 |
∴
| 1 |
| 2 |
| π |
| 3 |
| ||
| 2 |
由余弦定理可得:b2=a2+c2-2accosB=22+12-2×2×1×
| 1 |
| 2 |
∴b=
| 3 |
∵a2=b2+c2,
∴A=
| π |
| 2 |
又a=2c,
∴C=
| π |
| 6 |
∴tanC=
| ||
| 3 |
点评:本题考查了三角形面积计算公式、余弦定理、勾股定理的逆定理、直角三角形的边角关系,考查了推理能力和计算能力,属于中档题.

练习册系列答案
相关题目
如图程序运行后输出的结果为( )


| A、22;-22 |
| B、-22;22 |
| C、6;-6 |
| D、-6;6 |
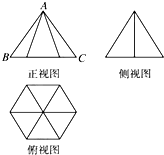 一个几何体的三视图如图所示,其中正视图中△ABC是边长为2的正三角形,俯视图为正六边形,求该几何体的侧视图的面积.
一个几何体的三视图如图所示,其中正视图中△ABC是边长为2的正三角形,俯视图为正六边形,求该几何体的侧视图的面积.
 已知程序如图:
已知程序如图: