题目内容
17.直线x-3y+3=0与圆(x-1)2+(y-3)2=10相交所得弦长为( )| A. | $\sqrt{30}$ | B. | $\frac{5\sqrt{3}}{2}$ | C. | 4$\sqrt{2}$ | D. | 3$\sqrt{3}$ |
分析 根据已知中圆的标准方程和直线的一般方程,代入圆的弦长公式,可得答案.
解答 解:圆(x-1)2+(y-3)2=10的圆心坐标为(1,3),半径r=$\sqrt{10}$,
圆心到直线x-3y+3=0的距离d=$\frac{|1-9+3|}{\sqrt{10}}$=$\frac{5}{\sqrt{10}}$,
故弦AB=2$\sqrt{10-\frac{25}{10}}$=$\sqrt{30}$,
故选A.
点评 本题考查的知识点是直线与圆的位置关系,熟练掌握圆的弦长公式,是解答的关键.

练习册系列答案
相关题目
12.下列命题中错误的是( )
| A. | 如果平面α外的直线a不平行于平面α,平面α内不存在与a平行的直线 | |
| B. | 如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么直线l⊥平面γ | |
| C. | 如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β | |
| D. | 一条直线与两个平行平面中的一个平面相交,则必与另一个平面相交 |
2.设全集为R,集合A={x|x2-16<0},B={x|-2<x≤6},则A∩(∁RB)等于( )
| A. | (-4,0) | B. | (-4,-2] | C. | (-4,4) | D. | (-4,-2) |
6.将函数$y=sin(2x+\frac{π}{6})$的图象向左平移m(m>0)个单位长度,得到函数y=f(x)图象在区间$[-\frac{π}{12},\frac{5π}{12}]$上单调递减,则m的最小值为( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$ |
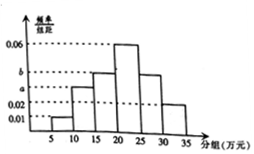 某统计部门就“A市汽车价格区间的购买意愿”对100人进行了问卷调查,并将结果制作成频率分布直方图,如图,已知样本中数据在区间[10,15)上的人数与数据在区间[25,30)的人数之比为3:4.
某统计部门就“A市汽车价格区间的购买意愿”对100人进行了问卷调查,并将结果制作成频率分布直方图,如图,已知样本中数据在区间[10,15)上的人数与数据在区间[25,30)的人数之比为3:4.