题目内容
在数列 中,
中,
(1)试判断数列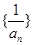 是否为等差数列;
是否为等差数列;
(2)设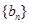 满足
满足 ,求数列
,求数列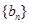 的前n项和
的前n项和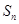 ;
;
(3)若 ,对任意n ≥2的整数恒成立,求实数
,对任意n ≥2的整数恒成立,求实数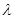 的取值范围.
的取值范围.
 中,
中,
(1)试判断数列
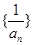 是否为等差数列;
是否为等差数列;
(2)设
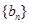 满足
满足 ,求数列
,求数列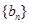 的前n项和
的前n项和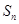 ;
;(3)若
 ,对任意n ≥2的整数恒成立,求实数
,对任意n ≥2的整数恒成立,求实数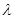 的取值范围.
的取值范围.(1)根据递推关系得到 ,从而结合定义来证明、
,从而结合定义来证明、
(2)
(3)λ的取值范围是(-∞, ].
].
 ,从而结合定义来证明、
,从而结合定义来证明、(2)

(3)λ的取值范围是(-∞,
 ].
].试题分析:
解: (1) ∵
 ,∴
,∴ ,∴由已知可得
,∴由已知可得 (n ≥ 2),
(n ≥ 2),故数列{
 }是等差数列,首项为1,公差为3.∴
}是等差数列,首项为1,公差为3.∴
(2)


上面两式相减得
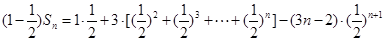
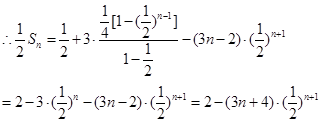

(3)将
 代入
代入 并整理得
并整理得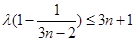 ,
,∴
 ,原命题等价于该式对任意n≥2的整数恒成立.
,原命题等价于该式对任意n≥2的整数恒成立.设
 ,则
,则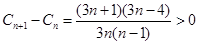 ,故
,故 ,
,∴Cn的最小值为C2=
 ,∴λ的取值范围是(-∞,
,∴λ的取值范围是(-∞, ].
].点评:主要是考查了数列的求和以及数列的单调性的运用,属于中档题。

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
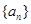 中,
中,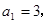 前
前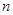 和
和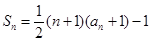
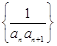 的前
的前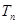 ,是否存在实数
,是否存在实数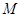 ,使得
,使得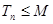 对一切正整数
对一切正整数 的前
的前 项和
项和 ,满足:
,满足: .
. ;
; 的满足
的满足 ,
, 为数列
为数列 的前
的前 .
. 的前n项和
的前n项和 ,则( )
,则( ) 的通项公式为
的通项公式为 ,那么满足
,那么满足 的整数
的整数 ( )
( )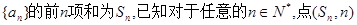 都在函数
都在函数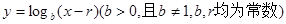 的图象上。
的图象上。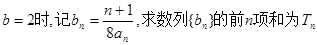 ;
;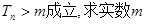 的取值范围。
的取值范围。 是函数
是函数 且
且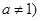 的图像上一点,等比数列
的图像上一点,等比数列 的前
的前 项的和为
项的和为 ;数列
;数列
 的首项为
的首项为 ,且前
,且前 满足
满足
 .
. 的前
的前 ,问
,问 的最小正整数
的最小正整数 的前
的前 项和
项和 满足
满足 ,等差数列
,等差数列 满足
满足 ,
, .
. ,数列
,数列 的前
的前 ,求证
,求证 .
. 中,
中, ,则
,则