题目内容
各项为正数的数列{an},其前n项的和为Sn,且Sn=(
+
)2(n≥2),若bn=
+
,且数列{bn}的前n项的和为Tn,则Tn=
.
| Sn-1 |
| a1 |
| an+1 |
| an |
| an |
| an+1 |
| 4n2+6n |
| 2n+1 |
| 4n2+6n |
| 2n+1 |
分析:由题意可得,
=
+
,结合等差数列的通项可求
,进而可求Sn,然后利用n≥2时,an=sn-sn-1式可求an,然后代入bn=
+
后,利用裂项求和即可求解
| sn |
| sn-1 |
| a1 |
| Sn |
| an+1 |
| an |
| an |
| an+1 |
解答:解:由题意可得,sn>0
∵Sn=(
+
)2(n≥2)
∴
=
+
即数列{
}是以
为公差以
=
为首项的等差数列
∴
=n
∴sn=n2a1,
∴当n≥2时,an=sn-sn-1=n2a1-(n-1)2a1=(2n-1)a1
当n=1时,适合上式
∴bn=
+
=
+
=1+
+1-
=2+2(
-
)
∴Tn=2n+2(1-
+
-
+…
-
)
=2n+2(1-
)
=2n+
=
故答案为:
∵Sn=(
| Sn-1 |
| a1 |
∴
| sn |
| sn-1 |
| a1 |
即数列{
| sn |
| a1 |
| s1 |
| a1 |
∴
| sn |
| a1 |
∴sn=n2a1,
∴当n≥2时,an=sn-sn-1=n2a1-(n-1)2a1=(2n-1)a1
当n=1时,适合上式
∴bn=
| an+1 |
| an |
| an |
| an+1 |
| 2n+1 |
| 2n-1 |
| 2n-1 |
| 2n+1 |
| 2 |
| 2n-1 |
| 2 |
| 2n+1 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴Tn=2n+2(1-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=2n+2(1-
| 1 |
| 2n+1 |
=2n+
| 2n |
| 2n+1 |
=
| 4n2+6n |
| 2n+1 |
故答案为:
| 4n2+6n |
| 2n+1 |
点评:本题主要考查了利用数列的递推公式构造等差 数列求解数列的通项公式,及数列的裂项求和,属于数列知识的综合应用

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 }满足a
}满足a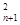 =2a
=2a +a
+a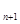 ,且a
,且a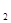 +a
+a =2a
=2a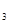 +4,其中n∈N
+4,其中n∈N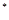 .
.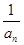 ,求数列{b
,求数列{b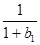 +
+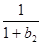 +…+
+…+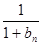 >
>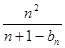 (n≥2).
(n≥2).