Question

已知函数f（x）=lnx-

1

2

ax²-2x（a＜0）．
（Ⅰ）若函数f（x）在定义域内单调递增，求实数a的取值范围；
（Ⅱ）若a=-

1

2

，且关于x的方程f（x）=-

1

2

x+b在[1，4]上恰有两个不等的实根，求实数b的取值范围；
（Ⅲ）设各项为正数的数列{a_n}满足a₁=1，a_n+1=lna_n+a_n+2（n∈N^*），求证：a_n≤2ⁿ-1．

Answer 1

分析：（1）对函数f（x）进行求导，令导数大于等于0在x＞0上恒成立即可．
（2）将a的值代入整理成方程的形式，然后转化为函数考虑其图象与x轴的交点的问题．
（3）设h（x）=lnx-x+1然后求导，可判断函数h（x）的单调性，再由数学归纳法得证．

解答：解：（I）f'（x）=-

ax2+2x-1

x

（x＞0）
依题意f'（x）≥0在x＞0时恒成立，即ax²+2x-1≤0在x＞0恒成立．
则a≤

1-2x

x2

=(

1

x

-1)2-1在x＞0恒成立，
即a≤((

1

x

-1)2-1)min（x＞0）
当x=1时，(

1

x

-1)2-1取最小值-1
∴a的取值范围是（-∞，-1]．

（II）a=-

1

2

，f（x）=-

1

2

x+b∴

1

4

x2-

3

2

x+lnx-b=0
设g（x）=

1

4

x2-

3

2

x+lnx-b(x＞0)则g'（x）=

(x-2)(x-1)

2x

列表：

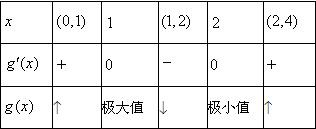
∴g（x）极小值=g（2）=ln2-b-2，g（x）极大值=g（1）=-b-

5

4

，
又g（4）=2ln2-b-2
∵方程g（x）=0在[1，4]上恰有两个不相等的实数根．
则

g(1)≥0 g(2)＜0 g(4)≥0

，得ln2-2＜b≤-

5

4

．

（III）设h（x）=lnx-x+1，x∈[1，+∞），则h'（x）=

1

x

-1≤0
∴h（x）在[1，+∞）为减函数，且h（x）_max=h（1）=0，故当x≥1时有lnx≤x-1．
∵a₁=1
假设a_k≥1（k∈N^*），则a_k+1=lna_k+a_k+2＞1，故a_n≥1（n∈N^*）
从而a_n+1=lna_n+a_n+2≤2a_n+1∴1+a_n+1≤2（1+a_n）≤…≤2ⁿ（1+a₁）
即1+a_n≤2ⁿ，∴an≤2ⁿ-1

点评：本题主要考查函数单调性与其导函数正负之间的关系，即当导函数大于0时原函数单调递增，当导函数小于0时原函数单调递减．