题目内容
各项为正数的数列{an},a1=a,其前n项的和为Sn,且Sn=(
+
)2(n≥2),则Sn=
| Sn-1 |
| a1 |
n2a
n2a
.分析:由各项为正数的数列{an},可知其前n项的和Sn>0,再利用等差数列的定义即可得出.
解答:解:∵an>0,∴Sn>0.
当n≥2时,由Sn=(
+
)2(n≥2),可得
=
+
,
又a1=a,∴
-
=
,
∴熟练{
}是以
为首项,
为公差的等差数列,
∴
=
+(n-1)
=n
,
∴Sn=n2a.
故答案为n2a.
当n≥2时,由Sn=(
| Sn-1 |
| a1 |
| Sn |
| Sn-1 |
| a |
又a1=a,∴
| Sn |
| Sn-1 |
| a |
∴熟练{
| Sn |
| a |
| a |
∴
| Sn |
| a |
| a |
| a |
∴Sn=n2a.
故答案为n2a.
点评:熟练掌握等差数列的定义是解题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
 }满足a
}满足a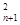 =2a
=2a +a
+a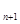 ,且a
,且a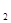 +a
+a =2a
=2a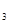 +4,其中n∈N
+4,其中n∈N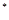 .
.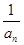 ,求数列{b
,求数列{b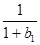 +
+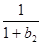 +…+
+…+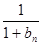 >
>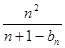 (n≥2).
(n≥2).