题目内容
9. 如图,平面PAC⊥平面ABC,点E、F、O分别为线段PA、PB、AC的中点,点G是线段CO的中点,AB=BC=AC=4,PA=PC=2$\sqrt{2}$.求证:
如图,平面PAC⊥平面ABC,点E、F、O分别为线段PA、PB、AC的中点,点G是线段CO的中点,AB=BC=AC=4,PA=PC=2$\sqrt{2}$.求证:(1)PA⊥平面EBO
(2)FG∥平面EBO.
分析 (1)推导出BO⊥AC,从而BO⊥面PAC,进而BO⊥PA,再求出OE⊥PA,由此能证明PA⊥平面EBO.
(2)连AF交BE于Q,连QO,推导出Q是△PAB的重心,从而FG∥QO,由此能证明FG∥平面EBO.
解答 证明:(1)由题意可知,△PAC为等腰直角三角形,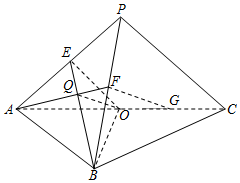
△ABC为等边三角形. …(2分)
因为O为边AC的中点,所以BO⊥AC,
因为平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,
BO?平面ABC,所以BO⊥面PAC. …(5分)
因为PA?平面PAC,所以BO⊥PA,
在等腰△PAC内,O、E为所在边的中点,所以OE⊥PA,
又BO∩OE=O,所以PA⊥平面EBO,…(8分)
(2)连AF交BE于Q,连QO.
因为E、F、O分别为边PA、PB、PC的中点,
所以$\frac{AO}{OG}$=2,且Q是△PAB的重心,…(10分)
于是$\frac{AQ}{QF}$=2=$\frac{AO}{OG}$,所以FG∥QO.…(12分)
因为FG?平面EBO,QO?平面EBO,所以FG∥平面EBO. …(14分)
点评 本题考查线面垂直、线面平行的证明,考查空间中线线、线面、面面间的关系等基础知识,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想,是中档题.

练习册系列答案
相关题目
19.如图是一个算法流程图,则输出的x的值是( )


| A. | 9 | B. | 10 | C. | 5 | D. | 7 |
20.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | $\frac{32π}{3}+32$ | B. | $\frac{32π}{3}+16$ | C. | 16π+32 | D. | 36π+16 |
4.已知点M在直线x+y+a=0上,过点M引圆x2+y2=2的切线,若切线长的最小值为2$\sqrt{2}$,则实数a的值为( )
| A. | ±2$\sqrt{2}$ | B. | ±3 | C. | ±4 | D. | ±2$\sqrt{5}$ |
1.某中学生物兴趣小组在学校生物园地种植了一批名贵树苗,为了解树苗生长情况,从这批树苗中随机测量了其中50棵树苗的高度(单位:厘米),把这些高度列成了如下的频率分布表:
(1)在这批树苗中任取一棵,其高度在85厘米以上的概率大约是多少?
(2)这批树苗的平均高度大约是多少?
(3)为了进一步获得研究资料,若从[40,50)组中移出一棵树苗,从[90,100]组中移出两棵树苗进行试验研究,则[40,50)组中的树苗A和[90,100]组中的树苗C同时被移出的概率是多少?
| 组别 | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 2 | 3 | 14 | 15 | 12 | 4 |
(2)这批树苗的平均高度大约是多少?
(3)为了进一步获得研究资料,若从[40,50)组中移出一棵树苗,从[90,100]组中移出两棵树苗进行试验研究,则[40,50)组中的树苗A和[90,100]组中的树苗C同时被移出的概率是多少?
19.已知抛物线C:x2=2py(p>0)的焦点为F,点P为抛物线C上的一点,点P处的切线与直线y=x平行,且|PF|=3,则抛物线C的方程为( )
| A. | x2=4y | B. | x2=8y | C. | x2=6y | D. | x2=16y |
