题目内容
5.已知tan($\frac{π}{4}$+α)=3$+2\sqrt{2}$,求$\frac{1-sin2α}{cos2α}$的值.分析 利用两角和的正切函数公式化简已知,解得tanα化简函数的表达式为正切函数的形式,然后求解即可.
解答 解:∵tan($\frac{π}{4}$+α)=3$+2\sqrt{2}$,可得$\frac{1+tanα}{1-tanα}$=3$+2\sqrt{2}$,
∴解得:tanα=$\frac{\sqrt{2}}{2}$.
∴$\frac{1-sin2α}{cos2α}$=$\frac{1-2sinαcosα}{co{s}^{2}α-si{n}^{2}α}$=$\frac{cosα-sinα}{cosα+sinα}$=$\frac{1-tanα}{1+tanα}$=$\frac{1-\frac{\sqrt{2}}{2}}{1+\frac{\sqrt{2}}{2}}$=3-2$\sqrt{2}$.
点评 本题考查两角和与差的三角函数,考查三角函数化简求值,考查计算能力,属于基础题.

练习册系列答案
相关题目
13.已知等比数列{an}的首项为1,若4a1,2a2,a3成等差数列,数列{$\frac{1}{{a}_{n}}$}的前n项和为Sn,则满足不等式Sn>$\frac{125}{63}$的n的最小值为( )
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
12.若集合M={1,2,3,4},N={x|x(x-3)<0},则M∩N等于( )
| A. | {1,2,3} | B. | {1,2} | C. | {x|1<x<3} | D. | {2,3,4} |
13.在△ABC中,BC=7,cosA=$\frac{1}{5}$,sinC=$\frac{2\sqrt{6}}{7}$.若动点P满足$\overrightarrow{AP}$=$\frac{λ}{2}$$\overrightarrow{AB}$+(1-λ)$\overrightarrow{AC}$(λ∈R),则点的轨迹与直线AB,AC所围成的封闭区域的面积为( )π
| A. | $3\sqrt{6}$ | B. | $4\sqrt{6}$ | C. | $6\sqrt{6}$ | D. | 12$\sqrt{6}$ |



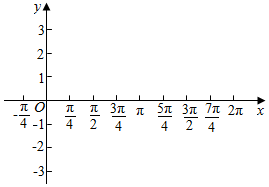 已知函数f(x)=3sin(x+$\frac{π}{4}$).
已知函数f(x)=3sin(x+$\frac{π}{4}$).