题目内容
已知x的一元二次方程x2+4x+m=0，
（1）若此方程有两个不同的实数解，求m的范围；
（2）若此方程的两个实数解分别为x1，x2，且x12+x22=18，求m的值及|x1-x2|的值．
（1）若此方程有两个不同的实数解，求m的范围；
（2）若此方程的两个实数解分别为x1，x2，且x12+x22=18，求m的值及|x1-x2|的值．
考点：二次函数的性质
专题：函数的性质及应用
分析：（1）由△＞0解出即可；（2）由韦达定理得出x1+x2=-4，x1•x2=m，从而求出m的值，代入|x1-x2|=
即可求出答案．
| (x1+x2)2-4x1x2 |
解答：
解：（1）∵此方程有两个不同的实数解，
∴△=16-4m＞0，解得：m＜4；
（2）∵x1+x2=-4，x1•x2=m，
∴x12+x22=(x1+x2)2-2x1x2=16-2m=18，解得：m=-1，
∴|x1-x2|=
=
=2
．
∴△=16-4m＞0，解得：m＜4；
（2）∵x1+x2=-4，x1•x2=m，
∴x12+x22=(x1+x2)2-2x1x2=16-2m=18，解得：m=-1，
∴|x1-x2|=
| (x1+x2)2-4x1x2 |
| 16-4×(-1) |
| 5 |
点评：本题考查了二次函数的性质，考查韦达定理，是一道基础题．
练习册系列答案
相关题目
程序如下：
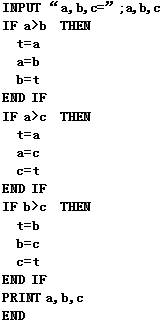
输入a=（-
）4，b=（-
）-4，c=log
，则运行结果为（ ）
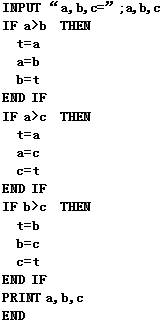
输入a=（-
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
A、（-
| ||||||||
B、（-
| ||||||||
C、（-
| ||||||||
D、（-
|