题目内容
三点A(x1,y1)、B(x2,y2)、C(x3,y3)共线的充要条件是( )A.(x2-x1)(y3-y1)=(x3-x1)(y2-y1)
B.(x2-x1)(x3-x1)=(y3-y1)(y2-y1)
C.x1y2-x2y1=0
D.x1y3-x3y1=0
思路解析:三点共线问题,用坐标表示的充要条件,首先考虑纯向量形式的充要条件,然后转化为坐标表示,即
=λ
(λ∈R)用坐标表示出来.
A、B、C三点共线
=λ
(λ∈R)
(x2-x1,y2-y1)=λ(x3-x1,y3-y1),
∴
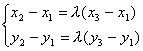
(x2-x1)(y3-y1)=(x3-x1)(y2-y1).
其他选项都错误.
故选A.
答案:A
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
+
=1上不同三点A(x1,y1)、B(4，9)、C（x2,y2）与右焦点F的距离成等差数列，求证：
-
=1上支上有不同的三点A(x1,y1)、B(x0,6)、C(x2,y2)与焦点F（0，5）的距离成等差数列.（1）求y1+y2的值；（2）求证：线段AC的中垂线经过某一定点，并求出这个定点坐标.
-
=1的一支上不同的三点A(x1,y1),B(x2，6），C(x3,y3)与焦点F(0,5)的距离成等差数列.
=1上有三点A(x1,y1)、B(4,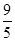
)、C(x2,y2)与右焦点F(4,0)的距离成等差数列，则x1＋x2的值为____________；