题目内容
在双曲线
-
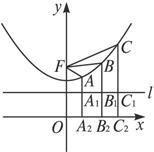
=1的一支上不同的三点A(x1,y1),B(x2，6），C(x3,y3)与焦点F(0,5)的距离成等差数列.
(1)试求y1+y3;
(2)证明线段AC的垂直平分线经过某一定点,并求该定点坐标.
1、12
2、当x=0时,y=
,故AC的垂直平分线过定点(0,).
解析:
(1)依题意,得B在双曲线上支上,故A、B、C三点都在双曲线上支上,且上准线的方程为y=
.
|AF|,|BF|,|CF|成等差数列,根据双曲线的第二定义,得
(6-)=
(y1-)+(y3-),故y1+y3=12.
(2)由点A、C在双曲线上,故
=1,
=1.两式相减,得
=0.
∴
.∴AC的垂直平分线的斜率为-
.
又AC的中点坐标为(
,6),
故AC的垂直平分线方程为y-6=-(x-),
当x=0时,y=
,故AC的垂直平分线过定点(0,).
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
-
=1的一支上不同的三点A(x1,y1),B(x2，6），C(x3,y3)与焦点F(0,5)的距离成等差数列.
=1的一支上有三个点A（x1，y1）、B（x2,6）、C(x3,y3)与焦点F（0,5）的距离成等差数列．
=-1的上支上有不同的三点A(x1,y1)、B(x2,6)、C(x3,y3)，与焦点F(0，5)的距离成等差数列.
-
=1的上支上有三点A(x1,y1),B(x2,6),C(x3,y3),它们与点F(0,5)的距离成等差数列.