题目内容
已知函数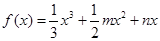 ,
,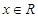 .
.
(Ⅰ)当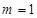 ,
,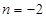 时,求
时,求 的单调区间;
的单调区间;
(2)当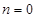 ,且
,且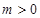 时,求
时,求 在区间
在区间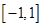 上的最大值.
上的最大值.
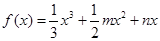 ,
,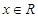 .
.(Ⅰ)当
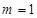 ,
,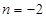 时,求
时,求 的单调区间;
的单调区间;(2)当
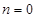 ,且
,且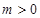 时,求
时,求 在区间
在区间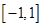 上的最大值.
上的最大值.(Ⅰ) 的单调递减区间
的单调递减区间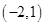 ;(Ⅱ)
;(Ⅱ) 在区间
在区间 上的最大值为
上的最大值为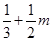 .
.
 的单调递减区间
的单调递减区间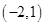 ;(Ⅱ)
;(Ⅱ) 在区间
在区间 上的最大值为
上的最大值为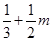 .
.试题分析:(Ⅰ)当
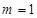 ,
,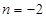 时,求
时,求 的单调区间,只需求出
的单调区间,只需求出 的导函数,判断
的导函数,判断 的导函数的符号,从而求出
的导函数的符号,从而求出 的单调区间;(Ⅱ)当
的单调区间;(Ⅱ)当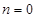 ,且
,且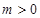 时,求
时,求 在区间
在区间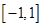 上的最大值,此题属于函数在闭区间上的最值问题,解此类题,只需求出极值,与端点处的函数值,比较谁大,就取谁,但此题,令
上的最大值,此题属于函数在闭区间上的最值问题,解此类题,只需求出极值,与端点处的函数值,比较谁大,就取谁,但此题,令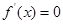 ,得
,得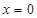 或
或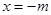 ,需对
,需对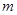 讨论,由于
讨论,由于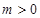 ,分
,分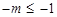 ,与
,与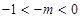 ,两种情况讨论,从而确定最大值,本题思路简单,运算较繁,特别是分类讨论,是学生的薄弱点.
,两种情况讨论,从而确定最大值,本题思路简单,运算较繁,特别是分类讨论,是学生的薄弱点.试题解析:(Ⅰ)当
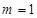 ,
,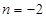 时,
时,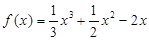 ,则
,则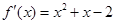 ,令
,令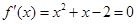 ,解得
,解得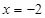 ,
,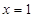 ,当
,当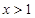 或
或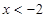 时,有
时,有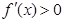 ; 当
; 当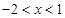 时,有
时,有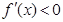 ,所以
,所以 的单调递增区间
的单调递增区间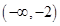 和
和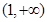 ,
, 的单调递减区间
的单调递减区间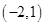 .
.(Ⅱ)当
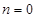 ,且
,且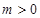 时,
时,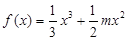 ,
,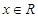 ,则
,则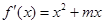 , 令
, 令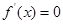 ,得
,得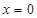 或
或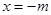 ,①当
,①当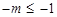 ,即
,即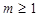 时,此时当
时,此时当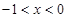 时,有
时,有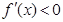 ,所以
,所以 在
在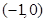 上为减函数,当
上为减函数,当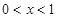 时,有
时,有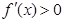 ,所以
,所以 在
在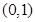 上为增函数,又
上为增函数,又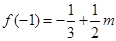 ,
,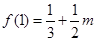 ,
,所以
 的最大值为
的最大值为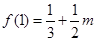 ;②当
;②当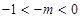 ,即
,即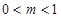 时,此时当
时,此时当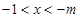 时,
时,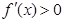 ;当
;当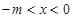 时,
时,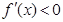 ;当
;当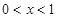 时,
时,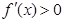 ;所以
;所以 在
在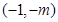 上为增函数,在
上为增函数,在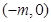 上为减函数,在
上为减函数,在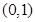 上为增函数,
上为增函数, 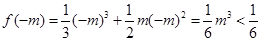 ,
, 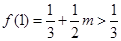 , 所以
, 所以 的最大值为
的最大值为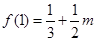 ,综上,
,综上, 在区间
在区间 上的最大值为
上的最大值为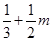 .
.
练习册系列答案
相关题目
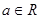 ,函数
,函数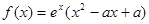 .
.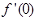 的值;
的值;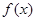 的单调区间.
的单调区间.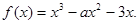
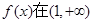 上是增函数,求实数
上是增函数,求实数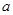 的取值范围.
的取值范围.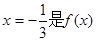 的一个极值点,求
的一个极值点,求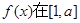 上的最大值.
上的最大值.
 .
. 时,求
时,求 的单调区间;
的单调区间; 在
在 单调递减,求实数
单调递减,求实数 的取值范围.
的取值范围.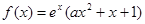 .
.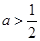 时,求
时,求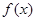 的单调区间;
的单调区间;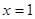 时,
时,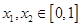 时,求
时,求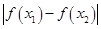 的取值范围.
的取值范围. .
. ,
,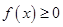 对一切
对一切 恒成立,求
恒成立,求 的最大值;
的最大值; ,且
,且 、
、 是曲线
是曲线 上任意两点,若对任意
上任意两点,若对任意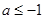 ,直线
,直线 的斜率恒大于常数
的斜率恒大于常数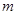 ,求
,求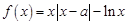 ,
,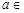
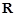 .
.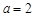 ,求函数
,求函数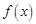 在区间
在区间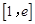 上的最值;
上的最值;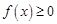 恒成立,求
恒成立,求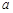 的取值范围.
的取值范围.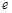 是自然对数的底数
是自然对数的底数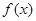 的导函数
的导函数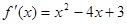 ,则
,则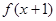 的单调递减区间是 .
的单调递减区间是 .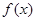 ,
,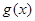 都是定义在R上的函数,
都是定义在R上的函数,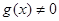 ,
,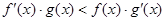 ,
,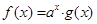
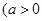 ,且
,且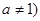 ,
,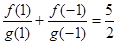 ,在有穷数列
,在有穷数列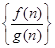
 中,任意取正整数
中,任意取正整数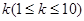 ,则前
,则前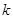 项和大于
项和大于 的概率是
的概率是