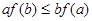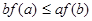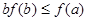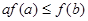题目内容
已知函数
 .
.
(1)当 时,求
时,求 的单调区间;
的单调区间;
(2)若函数 在
在 单调递减,求实数
单调递减,求实数 的取值范围.
的取值范围.

 .
.(1)当
 时,求
时,求 的单调区间;
的单调区间;(2)若函数
 在
在 单调递减,求实数
单调递减,求实数 的取值范围.
的取值范围.(1) 在
在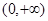 上单调递增.(2)
上单调递增.(2)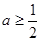 .
.
 在
在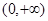 上单调递增.(2)
上单调递增.(2)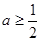 .
.试题分析:(1)通过“求导数,求驻点,分区间讨论”,可得函数的单调区间.也可利用导数大于0或小于0 ,解不等式,得到单调区间.
(2)问题转化成
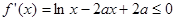 在
在 上恒成立,由
上恒成立,由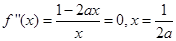 ,对
,对 进行分类讨论,求得其范围.
进行分类讨论,求得其范围.试题解析:(1)
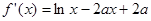 1分
1分 ,
,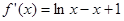 ,
,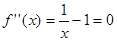 ,
,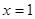 ,
,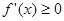 , 4分
, 4分 在
在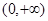 上单调递增 5 分
上单调递增 5 分(2)
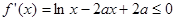 在
在 上恒成立,
上恒成立,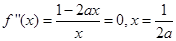
①
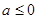 时,
时, 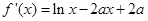 在
在 是增函数,其最小值为0,不合题意; 7分
是增函数,其最小值为0,不合题意; 7分②
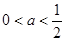 时,
时,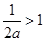 ,函数
,函数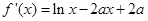 有最大值
有最大值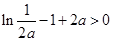 ,不合题意; 9分
,不合题意; 9分③
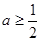 时,
时,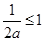 ,函数
,函数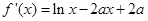 在
在 单调递增,在
单调递增,在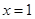 处取到最小值0; 11分
处取到最小值0; 11分综上:
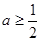 12分
12分
练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
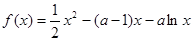 ,
,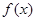 的单调区间;
的单调区间;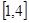 内的最小值为
内的最小值为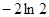 ,求
,求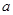 的值.(参考数据
的值.(参考数据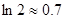 )
)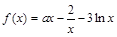 ,其中
,其中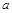 为常数.
为常数.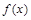 的图象在点
的图象在点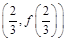 处的切线的斜率为1时,求函数
处的切线的斜率为1时,求函数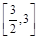 上的最小值;
上的最小值;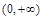 上既有极大值又有极小值,求实数
上既有极大值又有极小值,求实数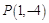 作函数
作函数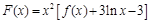 图象的切线,试问这样的切线有几条?并求这些切线的方程.
图象的切线,试问这样的切线有几条?并求这些切线的方程.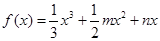 ,
,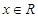 .
.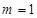 ,
,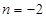 时,求
时,求 的单调区间;
的单调区间;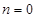 ,且
,且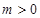 时,求
时,求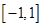 上的最大值.
上的最大值.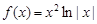 ,
,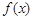 的奇偶性;
的奇偶性;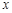 的方程
的方程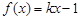 有实数解,求实数
有实数解,求实数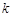 的取值范围
的取值范围 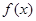 满足
满足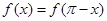 ,且当
,且当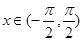 时,
时,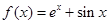 ,则( )
,则( )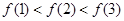
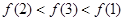
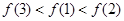
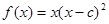 在
在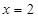 处有极大值,则常数
处有极大值,则常数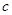 的值为________.
的值为________.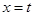 与函数
与函数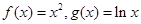 的图象分别交于点
的图象分别交于点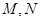 ,则当
,则当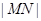 达到最小时
达到最小时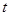 的值为( )
的值为( )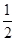
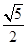
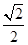
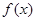 是定义在
是定义在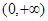 上的非负可导函数,且满足
上的非负可导函数,且满足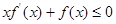 .对任意正数
.对任意正数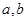 ,若
,若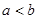 ,则必有( )
,则必有( )