题目内容
18.在抛物线y=4x2上有一点P,使这点到直线y=4x-5的距离最短,求该点P坐标和最短距离.分析 根据抛物线的方程设出点P的坐标,然后利用点到直线的距离公式表示出点P到直线y=4x-5的距离d,利用二次函数求最值的方法得到所求点P的坐标即可.
解答 解:设点P(t,4t2),点P到直线y=4x-5的距离为d,
则d=$\frac{|4t-4{t}^{2}-5|}{\sqrt{17}}$=$\frac{4(t-\frac{1}{2})^{2}+4}{\sqrt{17}}$,
当t=$\frac{1}{2}$时,d取得最小值,
此时P($\frac{1}{2}$,1)为所求的点,最短距离为$\frac{4\sqrt{17}}{17}$
点评 此题考查学生灵活运用点到直线的距离公式化简求值,掌握二次函数求最值的方法,是一道中档题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
6.已知F1、F2为双曲线C:x2-y2=2的左、右焦点,点P在C上,|PF1|=2|PF2|,则△F1PF2的形状为( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 等边三角形 |
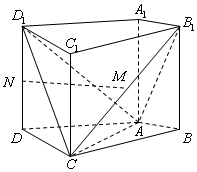 如图,在四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB⊥AC,AB=3,AC=AA1=6,AD=CD=5,且点M和N分别为B1C和D1D的中点.
如图,在四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB⊥AC,AB=3,AC=AA1=6,AD=CD=5,且点M和N分别为B1C和D1D的中点.