题目内容
一个袋中袋有5个形状大小完全相同的小球,其中红球有2个,编号分别为1,2;黑球有2个,编号分别为1,2;白球有一个,编号为1,现从袋中一次随机抽取2个球.
(1)求取出的2个球的颜色不相同的概率;
(2)求取得的球中有1号球的概率.
(1)求取出的2个球的颜色不相同的概率;
(2)求取得的球中有1号球的概率.
考点:列举法计算基本事件数及事件发生的概率
专题:概率与统计
分析:先列举出所有的基本事件,再分别找到(1)取出的2个球的颜色不相同基本事件,(2)取得的球中有1号球的基本事件,根据概率公式计算即可.
解答:
解:从袋中一次随机抽取2个球的基本情况有:(红1,红2),(红1,黑1),(红1,黑2),(红1,白1),(红2,黑1),(红2,黑2),(红2,白1),(黑1,黑2),(黑1,白1),(黑2,白1),共10种,
(1)取出的2个球的颜色不相同的基本事件有:(红1,黑1),(红1,黑2),(红1,白1),(红2,黑1),(红2,黑2),(红2,白1),(黑1,白1),(黑2,白1),共8种,
故取出的2个球的颜色不相同的概率为
=
,
(2)取得的球中有1号球的基本事件有::(红1,红2),(红1,黑1),(红1,黑2),(红1,白1),(红2,黑1),(红2,白1),(黑1,黑2),(黑1,白1),(黑2,白1),共9种,
故取得的球中有1号球的概率
(1)取出的2个球的颜色不相同的基本事件有:(红1,黑1),(红1,黑2),(红1,白1),(红2,黑1),(红2,黑2),(红2,白1),(黑1,白1),(黑2,白1),共8种,
故取出的2个球的颜色不相同的概率为
| 8 |
| 10 |
| 4 |
| 5 |
(2)取得的球中有1号球的基本事件有::(红1,红2),(红1,黑1),(红1,黑2),(红1,白1),(红2,黑1),(红2,白1),(黑1,黑2),(黑1,白1),(黑2,白1),共9种,
故取得的球中有1号球的概率
| 9 |
| 10 |
点评:本题考查概率的计算,考查学生的计算能力,确定基本事件的个数是关键.

练习册系列答案
相关题目
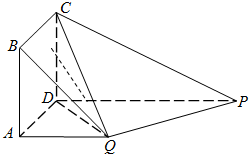 在如图所示的多面体中,四边形ABCD为正方形,四边形ADPQ是直角梯形,AD⊥DP,CD⊥平面ADPQ,AB=AQ=
在如图所示的多面体中,四边形ABCD为正方形,四边形ADPQ是直角梯形,AD⊥DP,CD⊥平面ADPQ,AB=AQ=| 1 |
| 2 |
(1)求证:PQ⊥平面DCQ;
(2)若AQ=2,求四面体C-BDQ的体积.
若U={1,2,3,4,5,6,7},A={3,4,6,7},B={3,5,6,7},则∁U(A∩B)=( )
| A、{1,2,4,5} |
| B、{2,6,8} |
| C、{1,3,5,7} |
| D、{1,2} |
