题目内容
答:![]() .
.
解:(1)解:设![]() 为函数
为函数![]() 图像的一个对称点,则
图像的一个对称点,则![]() 对于
对于![]() 恒成立.
恒成立.
即![]() 对于
对于![]() 恒成立,
恒成立,
![]() 由
由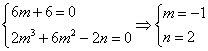 ,
,
故函数![]() 图像的一个对称点为
图像的一个对称点为![]() .
.
(2)是否存在常数![]() ,使得
,使得![]() 恒成立?
恒成立?
因为![]() 是奇函数,所以
是奇函数,所以![]() ,
,![]() ,则
,则![]() 恒成立。
恒成立。
特殊值赋值法:取![]() ,则
,则![]() ,所以只能取
,所以只能取![]() 。
。
现在说明当![]() 时,上式不恒成立。即
时,上式不恒成立。即![]() ,
,
比如取![]() ,上式为
,上式为![]() 不成立。
不成立。
故不存在符合题意的常数![]() 。
。
串题:并讨论是否存在常数![]() ,使得
,使得![]() (
(![]() )恒成立?
)恒成立?
分析:(1)当![]() 时,则
时,则![]() ,
,![]()
令![]()
![]() 时,
时,![]() ,所以
,所以![]() 单调递增,所以
单调递增,所以![]()
![]()
(2)当![]() 时,
时,![]()
当![]() 递增;当
递增;当![]() 递减。
递减。
![]() (该值小于7)
(该值小于7)![]()
综合上述可知: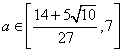
(3)函数![]() 的图像关于直线
的图像关于直线![]() 对称的充要条件是
对称的充要条件是![]()
①![]() 时,
时,![]() ,其图像关于
,其图像关于![]() 轴上任意一点成中心对称;关于平行于
轴上任意一点成中心对称;关于平行于![]() 轴的任意一条直线成轴对称图形;
轴的任意一条直线成轴对称图形;
②![]() 时,
时,![]() ,其图像关于
,其图像关于![]() 轴对称图形;
轴对称图形;
③![]() 时,
时,![]() ,其图像关于原点中心对称;
,其图像关于原点中心对称;
④![]() 时,
时,![]() 的图像不可能是轴对称图形。
的图像不可能是轴对称图形。
(可以画出函数的草图)
设![]() 为函数
为函数![]() 图像的一个对称点,则
图像的一个对称点,则![]() 对于
对于![]() 恒成立.
恒成立.
即![]() 对于
对于![]() 恒成立,
恒成立,
![]() 由
由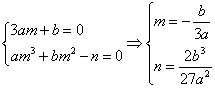 ,
,
故函数![]() 图像的一个对称点为
图像的一个对称点为![]() .
.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
某地区教研部门要对高三期中数学练习进行调研,考察试卷中某道填空题的得分情况.已知该题有两空,第一空答对得3分,答错或不答得0分;第二空答对得2分,答错或不答得0分.第一空答对与否与第二空答对与否是相互独立的.从所有试卷中随机抽取1000份试卷,其中该题的得分组成容量为1000的样本,统计结果如下表:
(Ⅰ)求样本试卷中该题的平均分,并据此估计这个地区高三学生该题的平均分;
(Ⅱ)这个地区的一名高三学生因故未参加考试,如果这名学生参加考试,以样本中各种得分情况的频率(精确到0.1)作为该同学相应的各种得分情况的概率.试求该同学这道题第一空得分不低于第二空得分的概率.
| 第一空得分情况 | 第二空得分情况 | |||||
| 得分 | 0 | 3 | 得分 | 0 | 2 | |
| 人数 | 198 | 802 | 人数 | 698 | 302 | |
(Ⅱ)这个地区的一名高三学生因故未参加考试,如果这名学生参加考试,以样本中各种得分情况的频率(精确到0.1)作为该同学相应的各种得分情况的概率.试求该同学这道题第一空得分不低于第二空得分的概率.