题目内容
一次数学考试后,对高三文理科学生进行抽样调查,调查其对本次考试的结果满意或不满意,现随机抽取100名学生的数据如下表所示:
(1)用分层抽样方法在感觉不满意的学生中随机抽取5名,理科生应抽取几人;
(2)在(1)抽取的5名学生中任取2名,求文理科各有一名的概率.
| 满意 | 不满意 | 总计 | |
| 文科 | 22 | 18 | 40 |
| 理科 | 48 | 12 | 60 |
| 总计 | 70 | 30 | 100 |
(2)在(1)抽取的5名学生中任取2名,求文理科各有一名的概率.
考点:等可能事件的概率,分层抽样方法
专题:概率与统计
分析:(1)计算分层抽样的抽取比例,根据比例计算理科不满意学生应抽取的人数;
(2)计算文科应抽取的人数,计算从5名学生中任取2名学生的取法种数,和其中文理各有一人的取法种数,代入古典概型概率公式计算.
(2)计算文科应抽取的人数,计算从5名学生中任取2名学生的取法种数,和其中文理各有一人的取法种数,代入古典概型概率公式计算.
解答:
解:(1)由题知感觉不满意的学生共有30人,抽取的比例为
=
,
所以理科生应抽取12×
=2人;
(2)文科生应抽取18×
=3人,
从5名学生中任取2名学生有
=10种取法;
其中文理各有一人的取法有
=6种,
∴文理科各有一名的概率为
=
.
| 5 |
| 30 |
| 1 |
| 6 |
所以理科生应抽取12×
| 1 |
| 6 |
(2)文科生应抽取18×
| 1 |
| 6 |
从5名学生中任取2名学生有
| C | 2 5 |
其中文理各有一人的取法有
| C | 1 2 |
| ×C | 1 3 |
∴文理科各有一名的概率为
| 6 |
| 10 |
| 3 |
| 5 |
点评:本题考查了分层抽样方法,考查了古典概型的概率计算.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
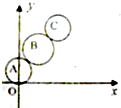 我们把圆心在一条直线上且相邻两圆彼此外切的一组圆 叫做“串圆”.在如图所示的“串圆”中,⊙A和⊙C的方程分别为x2+(y-1)2=2和(x-6)2+(y-7)2=2,则⊙B的方程为
我们把圆心在一条直线上且相邻两圆彼此外切的一组圆 叫做“串圆”.在如图所示的“串圆”中,⊙A和⊙C的方程分别为x2+(y-1)2=2和(x-6)2+(y-7)2=2,则⊙B的方程为