题目内容
已知等差数列{an}中a2=8前10项和S10=185.
(1)求通项an;
(2)若从数列{an}中依次取第2项、第4项、第8项、…、第2n项、…,按原来的顺序组成一个新的数列{bn},求数列{bn}的前n项和Tn.
(1)求通项an;
(2)若从数列{an}中依次取第2项、第4项、第8项、…、第2n项、…,按原来的顺序组成一个新的数列{bn},求数列{bn}的前n项和Tn.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)利用等差数列的性质求出第9项,然后求出公差,即可求通项an;
(2)利用已知条件求数列{bn}的通项公式,利用拆项法求解前n项和Tn.
(2)利用已知条件求数列{bn}的通项公式,利用拆项法求解前n项和Tn.
解答:
解:(1)∵S10=
且S10=185,a2=8
∴a9=29∴公差d=
=3
∴an=a2+(n-1)d=3n+2
(2)由题易知bn=a2n=3×2n+2
∴Tn=b1+b2+…+bn=3×(2+22+23+…+2n)+2n=6(2n-1)+2n=3×2n+1+2n-6.
| (a2+a9)•10 |
| 2 |
∴a9=29∴公差d=
| a9-a2 |
| 9-2 |
∴an=a2+(n-1)d=3n+2
(2)由题易知bn=a2n=3×2n+2
∴Tn=b1+b2+…+bn=3×(2+22+23+…+2n)+2n=6(2n-1)+2n=3×2n+1+2n-6.
点评:本题考查数列求和的方法拆项法的应用,等差数列的通项公式的求法,基本知识的考查.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
正四面体的内切球与外接球的半径的比等于( )
| A、1:3 | B、1:2 |
| C、2:3 | D、3:5 |
f(x)=xlnx在(0,+∞)上的最小值为( )
| A、e-1 |
| B、-e-1 |
| C、-1 |
| D、不存在 |
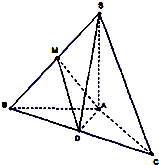 如图,在三棱锥S-ABC中,SA⊥平面ABC,AB=AC=1,SA=2,D为BC的中点.M为SB上的点,且AM=
如图,在三棱锥S-ABC中,SA⊥平面ABC,AB=AC=1,SA=2,D为BC的中点.M为SB上的点,且AM=