题目内容
13.若AB,AC,AD两两互相垂直,且AB=5,AC=4,AD=3,则三棱锥A-BCD的体积为10.分析 由题意画出图形,再由等积法求得三棱锥A-BCD的体积.
解答 解:如图,
∵AB,AC,AD两两互相垂直,且AB=5,AC=4,AD=3,
∴${V}_{A-BCD}={V}_{D-ABC}=\frac{1}{3}×\frac{1}{2}×5×4×3=10$.
故答案为:10.
点评 本题考查利用等积法求多面体的体积,是基础题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
8.若sinθ-cosθ=$\frac{1}{2}$,则sin($\frac{3π}{2}$-4θ)的值为( )
| A. | $\frac{{3\sqrt{7}}}{8}$ | B. | $-\frac{{3\sqrt{7}}}{8}$ | C. | $\frac{1}{8}$ | D. | $-\frac{1}{8}$ |
5.在三棱锥P-ABCD中,PA=PB=PC=2$\sqrt{6}$,AC=AB=4,且AC⊥AB,则该三棱锥外接球的表面积为( )
| A. | 4π | B. | 36π | C. | 48π | D. | 24π |
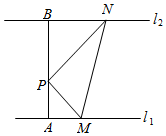 如图,P是两条平行直线l1,l2之间的一个定点,且点P到l1,l2的距离分别为PA=1,PB=$\sqrt{3}$,设△PMN的另两个顶点M,N分别在l1,l2上运动,设∠MPN=α,∠PMN=β,∠PNM=γ,且满足sinβ+sinγ=sinα(cosβ+cosγ).
如图,P是两条平行直线l1,l2之间的一个定点,且点P到l1,l2的距离分别为PA=1,PB=$\sqrt{3}$,设△PMN的另两个顶点M,N分别在l1,l2上运动,设∠MPN=α,∠PMN=β,∠PNM=γ,且满足sinβ+sinγ=sinα(cosβ+cosγ). 椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,右焦点为F,过点F的直线交椭圆于A,B两点,当A为下顶点时,|AF|=2.
椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,右焦点为F,过点F的直线交椭圆于A,B两点,当A为下顶点时,|AF|=2.