题目内容
(本题满分12分)如图,已知 , 四边形
, 四边形 是梯形,
是梯形, ∥
∥ ,
,  ,
, ,
, 

 中
中 点。
点。

(1)求证: ∥平面
∥平面 ;
;
(2)求异面直线 与
与 所成角的余弦值。
所成角的余弦值。

 , 四边形
, 四边形 是梯形,
是梯形, ∥
∥ ,
,  ,
, ,
, 

 中
中 点。
点。
(1)求证:
 ∥平面
∥平面 ;
;(2)求异面直线
 与
与 所成角的余弦值。
所成角的余弦值。
(1)证明: CE∥面PAB. (6分)
(2)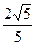 (12分
(12分
(2)
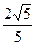 (12分
(12分(1)证明:取PA中点F,连结EF,BF,
∵E为PD中点,∴EF∥AD,且EF=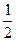 AD,
AD,
又BC∥AD,BC=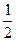 AD,∴EF∥BC,EF=BC,
AD,∴EF∥BC,EF=BC,
∴四边形BCEF为平行四边形,∴CE∥BF,
∵CE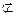 面PAB, BF
面PAB, BF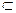 面PAB,∴CE∥面PAB. (6分)
面PAB,∴CE∥面PAB. (6分)
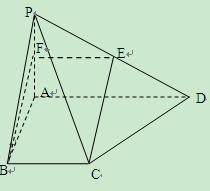
(2)由(1)CE∥BF,
∴∠FBA(或其补角)即为CE与AB所成角,
设PA=AB=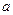 ,则在Rt
,则在Rt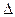 BAF中,AF=
BAF中,AF=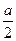 ,BF=
,BF=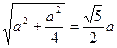 ,∴cosFBA=
,∴cosFBA=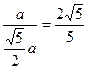 ,∴CE与AB所成角的余弦值为
,∴CE与AB所成角的余弦值为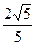 (12分
(12分
∵E为PD中点,∴EF∥AD,且EF=
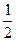 AD,
AD,又BC∥AD,BC=
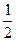 AD,∴EF∥BC,EF=BC,
AD,∴EF∥BC,EF=BC,∴四边形BCEF为平行四边形,∴CE∥BF,
∵CE
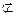 面PAB, BF
面PAB, BF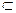 面PAB,∴CE∥面PAB. (6分)
面PAB,∴CE∥面PAB. (6分)
(2)由(1)CE∥BF,
∴∠FBA(或其补角)即为CE与AB所成角,
设PA=AB=
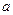 ,则在Rt
,则在Rt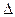 BAF中,AF=
BAF中,AF=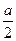 ,BF=
,BF=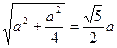 ,∴cosFBA=
,∴cosFBA=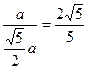 ,∴CE与AB所成角的余弦值为
,∴CE与AB所成角的余弦值为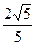 (12分
(12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 与
与 都是边长为2的正三角形,平面
都是边长为2的正三角形,平面 平面
平面 ,
, 平面
平面
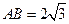 .
.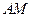 与平面
与平面 与平面
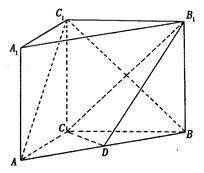
与平面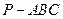 中,
中,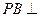 底面
底面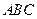 于
于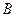 ,
,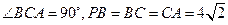 ,点
,点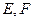 分别是
分别是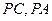 的中点,求二面角
的中点,求二面角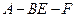 的余弦值.
的余弦值.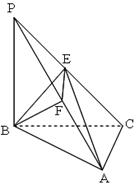
 ,底面对角线的长为
,底面对角线的长为 ,则侧面与底面所成的二面角等于 .
,则侧面与底面所成的二面角等于 . 中,已知棱
中,已知棱 的长为
的长为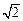 ,其余各棱长都为1,求二面角
,其余各棱长都为1,求二面角 的大小.
的大小. 中,
中, 与平面
与平面 所成的角的大小是( )
所成的角的大小是( ) B.arcsin
B.arcsin D.arccos
D.arccos