题目内容
下列参数方程(t为参数)与普通方程x2-y=0表示同一曲线的方程是( )
A、
| |||||||
B、
| |||||||
C、
| |||||||
D、
|
考点:参数方程化成普通方程
专题:选作题,坐标系和参数方程
分析:A、C项中的方程与方程y2=x表示的不是同一曲线;B中y∈[-1,1],均排除.
解答:
解:A、C项中的方程与方程y2=x表示的不是同一曲线;
B中,利用三角函数的性质知y∈[-1,1],均排除.
当x=tant时,根据y=x2可得:
y=tan2t
=
=
故选:D.
B中,利用三角函数的性质知y∈[-1,1],均排除.
当x=tant时,根据y=x2可得:
y=tan2t
=
| sin2t |
| cos2t |
=
| 1-cos2t |
| 1+cos2t |
故选:D.
点评:本题主要考查了抛物线的参数方程.解题的关键是看函数的值域和定义域、解析式是否一致.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
二次不等式ax2+bx+c≥0的解集为空集的条件是( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
已知△ABC的三个顶点A,B,C及所在平面内一点P满足
+2
+3
=
,则△BCP的面积与△ABP的面积之比为( )
| BC |
| BA |
| PB |
| 0 |
| A、2:1 | B、3:1 |
| C、3:2 | D、1:2 |
按流程图的程序计算,若开始输入的值为x=2,则输出的x的值是( )

| A、231 | B、156 |
| C、21 | D、15 |
已知复数z=a+
i在复平面内对应的点位于第二象限,且|z|=2,则复数z等于( )
| 3 |
A、-1+
| ||||
B、1+
| ||||
C、-1+
| ||||
D、-2+
|
设a=0.30.2,b=0.20.3,c=0.20.2,则a,b,c的大小关系是( )
| A、a>b>c |
| B、a>c>b |
| C、c>b>a |
| D、c>a>b |
已知P(-1,y)是角θ终边上一点,且sinθ=
,则y的值( )
2
| ||
| 5 |
| A、2 | B、-2 | C、±2 | D、1 |
若a>1,设函数f(x)=ax+x-2的零点为m,g(x)=logax+x-2的零点为n,则
+
的取值范围是( )
| 1 |
| m |
| 1 |
| n |
| A、(2,+∞) | ||
B、(
| ||
| C、(4,+∞) | ||
D、(
|
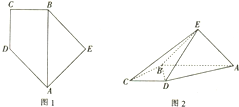 已知直角梯形ABCD的下底与等腰三角形ABE的斜边重合,AB⊥BC且AB=2CD=2BC(如图1),将此图形沿AB折叠成直二面角,连结EC、ED,得到四棱锥E-ABCD(如图2)
已知直角梯形ABCD的下底与等腰三角形ABE的斜边重合,AB⊥BC且AB=2CD=2BC(如图1),将此图形沿AB折叠成直二面角,连结EC、ED,得到四棱锥E-ABCD(如图2)