题目内容
(12分)已知函数f(x)=(2﹣a)(x﹣1)﹣2lnx,(a为常数,e为自然对数的底,e≈2.71828).
(1)当a=1时,求f(x)的单调区间;
(2)若f(x)>0在区间(0,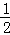 )上恒成立,求a的最小值.
)上恒成立,求a的最小值.
(1)f(x)的单调减区间为(0,2],单调增区间为(2,+∞);
(2)a的最小值为2﹣4ln2.
【解析】
试题分析:(1)先求函数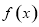 的导数
的导数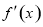 ,然后用导数
,然后用导数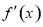 求函数
求函数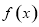 的单调区间;
的单调区间;
(2)对任意的x∈(0,),f(x)>0恒成立,即对x∈(0, ),a>2﹣
),a>2﹣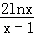 恒成立,令g(x)=2﹣
恒成立,令g(x)=2﹣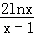 ,x∈(0,
,x∈(0, ),问题转化为求函数的
),问题转化为求函数的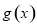 最值问题.
最值问题.
试题解析:【解析】
(1)当a=1时,f(x)=x﹣1﹣2lnx,则f′(x)=1﹣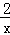 ,
,
由f′(x)>0,x>2;f′(x)<0,得0<x<2.
故f(x)的单调减区间为(0,2],单调增区间为(2,+∞);
(2)对任意的x∈(0,),f(x)>0恒成立,即对x∈(0, ),a>2﹣
),a>2﹣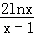 恒成立,
恒成立,
令g(x)=2﹣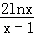 ,x∈(0,
,x∈(0, ),
),
则g′(x)=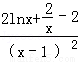 ,
,
再令h(x)=21nx+ ﹣2,x∈(0,
﹣2,x∈(0, ),则h′(x)=
),则h′(x)=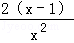 <0,
<0,
故h(x)在(0,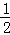 )上为减函数,
)上为减函数,
于是h(x)>h(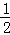 )=2﹣2ln2>0,
)=2﹣2ln2>0,
从而,g′(x)>0,于是g (x)在(0,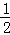 )上为增函数,
)上为增函数,
所以g(x)<g(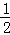 )=2﹣41n2,
)=2﹣41n2,
故要使a>2﹣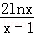 恒成立,只需a≥2﹣41n2.
恒成立,只需a≥2﹣41n2.
∴a的最小值为2﹣4ln2.
考点:1、导数在研究函数性质中的应用;2、等价转化的思想.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
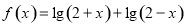 .
. 的定义域;
的定义域;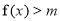 有解,求实数
有解,求实数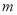 的取值范围.
的取值范围. 的虚部是( )
的虚部是( ) B.
B. C.
C. D.
D.

 B.
B.
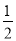 D.
D.
 的虚部是( )
的虚部是( ) B.
B. C.
C. D.
D.
 ),则下列结论正确的是( )
),则下列结论正确的是( ) ,0)对称
,0)对称 ]上为增函数
]上为增函数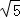 的概率为 _________ .
的概率为 _________ .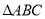 中,设角
中,设角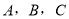 的对边分别为
的对边分别为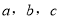 ,且
,且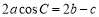 .
.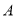 的大小;
的大小;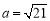 ,
,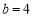 ,求边
,求边 的大小.
的大小.